Em Teoria dos Números, algo que ajuda muito na hora de resolver problemas é a famosa “aritmética modular”, que é equivalente à análise de restos. Você pode ver o básico sobre aritmética modular e relações de congruência aqui, no post antigo do Eduardo. Entretanto, hoje vamos mais a fundo: saberemos como determinar quais números têm um inverso modular, além de alguns teoremas e aplicações importantes, porém mais recentes. Mas, antes, vamos relembrar o básico:
Definição 1: Dizemos que dois inteiros a,b são congruentes módulo m se m|a – b. (Escrevemos a ≡b (mód m)). Analogamente, se a,b são congruentes módulo m, eles têm o mesmo resto na divisão por m.
Reparem que as relações de congruência satisfazem todas as propriedades básicas de operações com inteiros:
Proposições Básicas: Se a≡b mod m e c ≡ d mod m, então a+c≡b+d mod m, a – c ≡ b – d mod m, ac ≡ bd mod m.
Exemplo Básico:
Resolução: Essa conta não parece muito “apetitosa” de se fazer. Portanto, vamos apenas analisar os restos das potências de 3 mód 7:
E, assim, temos nossa repetição. Logo, agora nossa tarefa é determinar o resto de
Mas
Logo, como 323 é ímpar, 5323 deve deixar resto 5 módulo 6. Assim, temos que nossa tarefa é equivalente a achar o resto de 35 módulo 7, que sabemos ser 5. Portanto,
Agora, podemos prosseguir à parte interessante:
Teorema de Invertíveis: Um número inteiro a é invertível módulo n quando existe b tal que ab ≡ 1 mod m. Então, todos os números invertíveis módulo m são os coprimos com m (ou seja, mdc(a,m) = 1).
Demonstração: Suponhamos mdc(a,m) ≠ 1, a<m. Então, se
O que significa que uma combinação linear de a,m tem que dar 1. Absurdo, pois a menor combinação linear que pode ocorrer entre dois números é seu mdc, que, neste caso, é diferente de 1. ■
Corolário: Todo inteiro m admite φ(m) invertíveis módulo m, onde φ(m) é o número de primos com m. ■
Com este teorema em mãos, vamos ao famoso
Teorema de Wilson: Seja p primo maior que 2. Então (p – 1)! ≡ -1 mod p.
Demonstração: Temos que todos os inteiros mód p são invertíveis, mas apenas dois destes são o inversos deles mesmos: 1 e -1. Mas isto tem que ser demonstrado:
Se
Então
Mas p é primo, e ambas as parcelas, menores que p. Logo, seu produto tem de ser igual a zero, gerando que x=1 ou x = -1.
Com isso, todos os inteiros módulo p ao serem multiplicados, com exceção do 1 e do -1, encontrarão seu inverso multiplicativo, e resultarão em 1 mod p. Ao multiplicar esses “uns” pelo um e pelo -1, obtemos -1. Mas a multiplicação de todos os inteiros menores de p é justamente (p – 1)!, o que completa a prova. ■
Corolário:
Demonstração: Temos que
Logo,
Como queríamos demonstrar. ■
Com este teorema em mãos, podemos aplicá-lo a alguns problemas:
Problema 1: Mostre que, p primo maior que 3, então
Resolução: Para este problema, precisaremos de um importante lema:
Se o leitor quiser, este pode demonstrá-lo utilizando indução. Porém, para poupar os detalhes da demonstração, prossigamos. Ao diminuir 2, teremos apenas fatores “múltiplos” de p². Isto é óbvio, pois p é primo. Assim, tudo que temos que fazer é demonstrar que
Mas isto é fácil: Reparemos que todos os k’s têm um inverso, digamos, rk. Assim, Podemos escrever
Mas os rk são apenas uma reordenação dos números de 1 a p – 1. Logo, Esta é a soma de todos os quadrados de números de um a n, que se dá por
Logo, no nosso caso,
Que é, de fato, múltiplo de p. ■
É óbvia, depois desse exemplo, a importância dos inversos multiplicativos módulo m. Agora, vamos a mais um teorema que ajuda muito na hora de resolver problemas deste tipo: o teorema de Euler-Fermat.
Teorema de Euler: Seja a um inteiro positivo e m outro inteiro positivo com mdc(a,m) = 1. Então, sempre vale que
Demonstração: Comecemos observando que se são os números primos com m menores que m, então eles são todos invertíveis, e representam todos os invertíveis módulo m. Logo, se selecionarmos a tal que mdc(a,m) = 1, então
também representará todos os invertíveis módulo m. Assim, se multiplicarmos todos os números deste conjunto e analisarmos o produto módulo m, teremos
Como queríamos demonstrar. ■
Corolário (Teorema de Fermat): É válido para todo a que
Demonstração: Para a múltiplo de p, é óbvio. Para todos os outros, como mdc(a,p)=1, então podemos aplicar diretamente o teorema acima para obter ap – 1 ≡ 1 mod p, e, multiplicando por a dos dois lados, obtemos a relação desejada. ■
Agora, vamos ao exemplo ilustrativo:
Problema 2: (OIbM 2001) Demonstrar que para todo n inteiro positivo existe 2m com m inteiro positivos tal que este tenha pelo menos 2n/3 – 1 zeros consecutivos dentre suas n últimas casas decimais.
Resolução: Sabemos que
Pelo teorema de Euler. Assim,
Agora, sabemos que 2n das ultimas casas decimais do número estão ocupadas com algarismos não nulos (na verdade, nem todos são não-nulos, mas eles bloqueiam a nossa sequência de zeros, e é isso que importa). Mas
Logo, eles bloqueiam no máximo n/3 +1 casas do final do número (pois n/3,quando não é inteiro, arredonda a potência de 10 para cima). Logo, Temos que pelo menos 2n/3 – 1 zeros consecutivos serão mantidos.
Ou seja, para todo n inteiro positivo, m = φ(5n) + n = 4.5n – 1 + n satisfaz o enunciado. ■
Observação: Este problema é clássico em teoria dos números; Várias versões envolvendo números de zeros ao final de certa potência de 2 são muito amplamente conhecidas, esta é a generalização deste problema.
Bom, espero que tenham gostado e entendido tudo que foi dito neste post, embora não tenha sido muito detalhado. Se você não está muito familiarizado com congruências, volte ao topo do post e veja o primeiro post sobre congruências, do Eduardo.
Lembre-se! Sua opinião é muito importante para sabermos sobre a qualidade do nosso trabalho. Avalie o post abaixo, não demora nada. Se quiser se expressar mais livremente, os comentários são incentivados por nós, donos do blog! Apenas lembre-se de ser educado na sua crítica ou sugestão.
Fontes:
MARTINEZ, Fabio Brochero, MOREIRA, Carlos Gustavo, SALDANHA, Nicolau, TENGAN, Eduardo. Teoria dos Números: Um passeio com primos e outros números familiares pelo mundo inteiro. Projeto Euclides, Brasil, 2010.



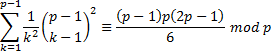
Parabéns pelo blog.
ResponderExcluirUma pequena correção: o meu livro acima em colaboração com o Fabio, o Nicolau e o Tengan foi publicado pela coleção Projeto Euclides, do IMPA, e não pela SBM (embora ele possa ser comprado na SBM).
Abraços,
Gugu
Olá professor! Erro corrigido. Tenha certeza de que estamos muito felizes de ter seu comentário aqui.
ResponderExcluirAbraços,
Eduardo
Não entendi como nem porque foi usado o mod6 se estava sendo usado o mod7! alguém pode me explicar?
ResponderExcluirOlá,
ExcluirO mod 6 foi usado pois as potências de 3 se repetem com período 6 no mod 7. Logo, temos que analisar o EXPOENTE mod 6 para ver como a potência em si vai se comportar mod 7.
Espero ter ajudado,
João Pedro.
Que bosta! não sabem explicar nada, aposto que o texto nem é autoral
ResponderExcluira resposta do primeiro problema esta errada.
ResponderExcluirAlguém pode dar uma dica para encontrar um k positivo tal que 5^k-97 seja múltiplo de 1001?
ResponderExcluirObrigado