Aplicação da Derivada (Parte 1)

Esse post será dedicado ao estudo da primeira das aplicações da derivada (além da Série de MacLaurin): Achar máximos e mínimos de uma função.
Para achar o máximo/ mínimo de uma função, teremos de analisar alguns exemplos:

Reparem que, quando há um máximo/mínimo local (ou global) da função, temos que ter uma parte (local) da curva em que não haja pontos maiores/menores do que este. Vemos, com o exemplo da curva acima, que se forma uma pequena “barriga” virada para cima (quando o ponto é máximo) ou para baixo (quando o ponto é mínimo) quando essas ocasiões acontecem. No ponto mais alto/baixo da curva, temos que a tangente ao ponto é horizontal, ou seja, ela é paralela ao eixo dos X.

O que acontece quando uma reta é paralela ao eixo dos X?

Essa reta tem equação , sendo uma constante. Ou seja, seu coeficiente angular é igual a zero (a equação poderia ser escrita como 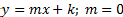). Como essa reta é tangente à função, seu coeficiente angular é dado pela derivada da função.

Figura 1: Função e reta tangente ao seu ponto máximo.
Que conclusão tiramos disso tudo?
Concluímos que, quando há um ponto máximo ou mínimo de uma função, sua derivada primeira se iguala a zero, ou seja, para acharmos os pontos máximos e mínimos de uma função, derivamos esta e igualamos sua derivada a zero, ou

Esse fato pode nos dar o ponto máximo ou mínimo quando a função é continuamente diferenciável, mas, em casos como da função a seguir, essa fórmula não se enquadra tão bem:

Como se pode ver, essa função, obviamente, tem ponto mínimo o ponto Mas, nesse ponto, a função não tem derivada, pois este é um ponto de inflexão entre duas funções. A derivada da primeira parte da função é , ou seja, essa função não “tem” ponto mínimo.
Já a segunda, derivando, possui ponto mínimo em . Isso quer dizer, automaticamente, que esse ponto é mínimo da função toda? Não! Para isso, temos que fazer a intercessão das duas funções, como abaixo:
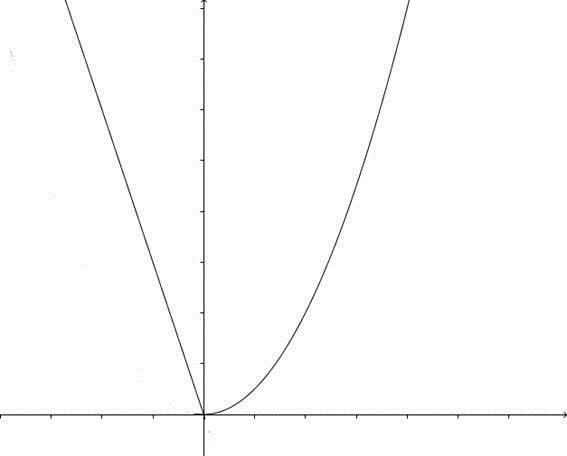
As nossas suspeitas se confirmam, e o ponto é mesmo o ponto mínimo da nossa função. Agora, alguns exemplos:
Exemplo 1: Temos um arame de 100 metros de comprimento. Queremos Dobrá-lo de forma a formar um quadrado e um círculo. Qual a área de cada figura, se quisermos obter a maior soma das áreas possível?
Solução: Inicialmente, montemos:


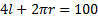
Agora, tudo o que temos a fazer é substituir uma das duas variáveis ( ou ). Suponha que substituamos o




Como a soma tem de ser máxima, derivamos, obtendo:


Entretanto, esse valor de nos dá um valor mínimo da função. Como vamos resolver?
É simples: é só estabelecermos o intervalo no qual a função está contida, que vai desde o valor a quando que é

Logo percebemos que, nesse intervalo, há dois pontos de máximos locais: e 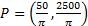. Aproximando, temos , ou seja, a função tem máximo total em
Exemplo 2: (Problema clássico de Física) Um projétil perfeito é lançado formando certo ângulo com a horizontal. Sabendo


Sendo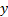 e altura e distância, respectivamente, calcule qual o ângulo que tornará:
a) A altura máxima
b) A distância máxima
Solução:
a) Para isso, apenas derivamos a função da altura, em relação à variável , ficando com

(consideramos e como constantes)
(a derivada do seno é o cosseno, como será demonstrado futuramente)
O único ângulo que torna o cosseno igual a zero é o de Ou seja, o ângulo de lançamento, para que a altura seja máxima, deve ser de .
b) Consideremos e a distância entre as raízes da função que dá o valor de . Temos, então:


Substituindo em , obtemos

Mas como , e substituindo , obtemos

Derivando (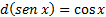 ), temos:



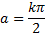
Como o número entre que se adapta é , então vemos que esse é o resultado.
Antes de terminar, vamos voltar à substituição que fizemos: . Então, temos que .
Ou seja, o ângulo que determina um alcance máximo é o de .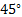
Espero que tenham entendido, pois esse é um dos assuntos principais em qual a derivada é usada.

Se você gostou do blog, inscreva por e-mail e no blog para receber as novas atualizações e curta nossa página no Facebook. Todas essas opções se encontram na barra lateral do blog e abaixo da postagem. Para melhorar a qualidade de nossas postagens avalie o conteúdo aqui embaixo. É rapidinho! Lembre-se que todo tipo de comentário que respeitar as regras é bem vindo.

Até mais!