Aula sobre Derivadas

 

Esse post vai ser dedicado a ensinar o que é a derivada, uma matéria essencial do cálculo e de todos os cursos superiores que envolvam matemática. Aqui vai: Imagine uma função , contínua, através da qual podemos traçar uma reta tangente, como segue na figura 1

 

 

 

 

 

 

 

 

Como qualquer reta, esta tem equação . Como já se sabe o valor de é , sendo e são a diferença entre as coordenadas de dois pontos por qual ela passe. Agora, imaginemos uma secante à mesma função.

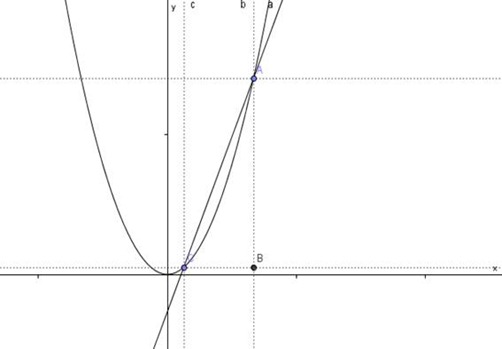Observamos que, à medida que a distância CB diminui a distância AB também diminui. Na verdade, chamemos o Ponto C de , já que ele pode ser variado, e, como está sobre a função , tem o parâmetro . Então, como o ponto A também está com abscissa , pois dista da abscissa de C. Como A se situa na função , então sua ordenada é . Então temos que o coeficiente angular da secante é

 

 

Agora retomemos à tangente. Como podemos ver, a distância de , causando, assim, que o coeficiente angular da tangente é

 

 

Ou seja, o coeficiente angular da tangente é o coeficiente angular da secante, à medida tende a 0. Essa é a derivada de uma função, representada por

 

 

A derivada também é chamada de taxa de variação de uma função.

 

Exemplo 1: Qual a equação da tangente à função no ponto com abscissa que vale 5?

Solução: Primeiro, derivamos a função. Obtemos:

 

 

Depois, como a abscissa vale 5, substituímos, obtendo

 

 

A equação da tangente é

 

 

Como, quando a reta tangencia a curva, a função e a derivada se igualam, tendo

 

Então, temos que a equação da tangente é

 

Exemplo 2: Dada uma função polinomial , calcule sua derivada.

 

Solução: Derivaremos, então:

 

 

Como o único termo dessa soma que não é multiplicado por é o primeiro, que é

 

 

 

,então este é o único que “resta” quando aplicamos o limite, ou seja,