Nesse, vou examinar o dito Sofisma Algébrico. Há alguns problemas no final:
Enunciado 1: Dados os números "a" e "b", sendo![clip_image002[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhXCupVdo_D9UwfBM24acUzKlSnmKhSf9YRiHBXqs5-CUTBdNq7zDpW4rXdb03MjKih2Lg2WDNLAIAqy4COQs6BgX49b7FmQXxZt_tVCyNxaO2lEBlnVa9tNvrdOLEG0CBRjchQfqZX0O4/?imgmax=800 "clip_image002[6]")
. “Provaremos” que a=b.
Primeiro, temos que![clip_image002[8]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjozUcl2eDNnLCsED-OMKvAHMF3qviGyvHkSqbpBIJ8-md0U3ivlz1oCx2suWdVemZW6ACnOf19Fns8NhygCWJ3u7HTTRqpyLASi8e21aNLxCi2_rbFkxJA52JT3ZQHDCOnnrdl1yesPxk/?imgmax=800 "clip_image002[8]")
.
Depois, podemos arrumar, botando em evidência os termos, com
![clip_image002[10]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjbKNVpmkA0SxNHzSEu-H0xHS_TFxBCvrj3bbPVON5A4JozRFx8kqbgecT_W7sx0tPVVlOfNPoc4ksv63h6dqH6Xk8gFEsWh9EYb5uc5HDdKnVFWUb9Cn2DVQ_6_mgwskiVdcvZAOz7o-Q/?imgmax=800 "clip_image002[10]")
Então, dividindo ambos os membros por (1-1), obtemos
a=b
, que é a contradição que queríamos mostrar.
Problemas:
2) Ache o erro no Sofisma Algébrico, evidenciando-o.
3) (Desafio, opcional) Ache o erro utilizando-se de congruências, a fim de provar que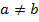
é a escolha verdadeira.
Enunciado 1: Dados os números "a" e "b", sendo
![clip_image002[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhBfdGaeYkKz5XUqnU1yK5-7pW27-DIHF7SiNvcMkQpiiBXG_bzDU8WdKCky0XpLKrQH0oaJQt0su6uB0HLMnDH1E43pAzZidWwayoXmXLL3GK-j1qk1ndZLigiF9SHglpzhR9u1rwnQt8/s1600-h/clip_image002%5B6%5D%5B2%5D.gif "clip_image002[6]"){kind=small}
. “Provaremos” que a=b. Primeiro, temos que
![clip_image002[8]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEij44dcmXQukcndz4NkK3nWeMr_BWjd8KgiUGg4NczPAjoxEEBByuuq4tX_cq2nVOA8W1ZUR0Gkl52G9u10U_tcYgV9QO8xEs5jCqobSjvM1e4mN-WOOvLRho89Y6xljN8EGwGmZgKxZHg/s1600-h/clip_image002%5B8%5D%5B2%5D.gif "clip_image002[8]"){kind=small}
. Depois, podemos arrumar, botando em evidência os termos, com
![clip_image002[10]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhKhpN-sQrNsTg1E_XlPh4hGFZb6guvZZ9EJfoJRmTRXTVSGlm8oxFW6Yn7PL43VkGoQP4l7-DQ2hqTyo4naiakmp4biHThEfH66XLQtUj0tU2xOAK4hm4HYEV0vXVtRqNXyMo6TYMnxPI/s1600-h/clip_image002%5B10%5D%5B2%5D.gif "clip_image002[10]"){kind=small}
Então, dividindo ambos os membros por (1-1), obtemos
a=b
, que é a contradição que queríamos mostrar.
Problemas:
2) Ache o erro no Sofisma Algébrico, evidenciando-o.
3) (Desafio, opcional) Ache o erro utilizando-se de congruências, a fim de provar que
é a escolha verdadeira.
isso é muito facil
ResponderExcluirDe fato, é uma postagem antiga. De uma olhada no resto do nosso blog e nossos parceiros. Deve ter algo que você goste.
ExcluirAbraços!
Eduardo.