A Área Do floco de neve de Von Koch

Seja o seguinte triângulo eqüilátero, aonde se fazem seguidas iterações, construindo novos triângulos, cujos lados depois desta iteração valem um terço do lado anterior.
Nesse triângulo fractal que obtemos, vamos demonstrar uma fórmula para sua área quando o número de iterações chega próximo ao infinito
Como cada triangulo tem o lado do anterior dividido por 3 para formar o lado dos tri}ângulos da iteração seguinte, e a área do triângulo eqüilátero é igual a

Temos que a área da unidade de cada triângulo, ou seja, de cada um dos triângulos resultantes após a iteração é dada por

Sendo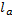 o lado do triângulo anterior. Já que todo lado é seu anterior dividido por um terço, analisemos:
O lado depois de uma iteração vale

Depois de duas iterações, fica

Depois de três, temos

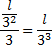
Ou seja, podemos deduzir que depois de n iterações teremos

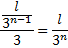
Substituindo na fórmula em (1), temos

Sendo

Temos

Mas essa fórmula só nos dá a área de um dos triângulos depois da iteração, e não de todos. Para achar a área de todos os triângulos daquela iteração, multiplicamos a fórmula da área pelo número de triângulos. Analisemos o número de triângulos: depois de uma iteração, temos 3 triângulos. A partir daí, cada triângulo de iteração “gera” quatro outros triângulos. Podemos deduzir, então, que o número de triângulos em cada iteração é de

Sendo n o número de iterações. A área somada dos triângulos daquela iteração é, então

Achamos, então, a área de um grupo dos triângulos em certa iteração, para n diferente de zero, pois quando n é igual a zero, a área diverge do valor que deveríamos obter. Para acharmos a soma de todos os triângulos em todas as iterações, temos

Para simplificarmos, fazemos

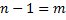
Obtemos, então

Depois dessa redução, vemos que essa expressão é a de uma soma dos termos de uma progressão geométrica de razão dois nonos. Agora, apenas aplicaremos a fórmula da soma dos termos de uma P.G. e um pouco da noção de limites. Esta fórmula diz que

Quando q é menor que 1 e n tende ao infinito, temos

Pois, como q é menor que 1, quando ele é potenciado um número grande de vezes ele acaba próximo de 0. Na nossa expressão, logo vemos que o termo inicial é

Agora, aplicando a fórmula para reduzir a expressão, obtemos

Somando ao termo em que o número de iterações é igual a zero (A), temos que a fórmula para a área total é

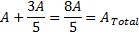
E essa é a área do floco de neve de Koch.