Números Complexos e a Unidade Imaginária–Parte 2

Como já dito anteriormente, um número complexo é qualquer número que contenha certa parte real e certa parte contendo a unidade imaginária. Agora, imaginemos um plano que associa cada número complexo a um ponto neste. Neste plano, o eixo dos “x” seria a parte real do número complexo, e o eixo dos “y” seria a parte imaginária. Ou seja, um ponto qualquer

seria a representação do número complexo . Veja a imagem abaixo:

Agora, vemos que o seu módulo (ver edição anterior) é a distância entre a origem e o próprio ponto. Introduzindo agora um novo conceito, temos que o ângulo (medido no sentido anti-horário) entre o módulo do número complexo e o eixo das abscissas é o argumento desse número. Essa propriedade é incrivelmente importante para a álgebra dos números complexos, pois ela definirá a potência de números complexos, radiciação de números complexos, a forma polar de números complexos e até o número de raízes que qualquer número complexo pode ter. Essas primeiras propriedades estão todas abaixo.

Representação Geométrica do Complexo (coordenadas polares):

No plano complexo, o eixo dos x representa a parte real do número complexo. Já o eixo dos y representa a parte imaginária. Então, cada número complexo pode ser representado por um ponto aonde é o número complexo em questão. A distância entre a origem pode ser dada pelo teorema de Pitágoras:

Que é chamado o módulo de z. Com isso, podemos expressar o número complexo de acordo com o ângulo que seu módulo faz com o eixo dos x.

O seno de teta pode ser definido como 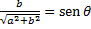. Então, b = Já o cosseno pode ser definido como . Então, temos a=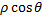. Substituindo no número complexo temos

Potenciação e Radiciação de Números Complexos

Teorema 1: todo complexo pode ser escrito como

Demonstração: Podemos escrever a potência de e da seguinte maneira

Para , temos

Por causa das propriedades da unidade imaginária:







Sendo , sendo 4k o múltiplo de 4 mais próximo de . Então, podemos propor que

Mas, notemos que:



E que:



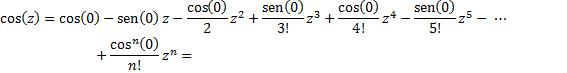
Daí, a expressão vira:


Podemos substituir em (1) , para obter

Fórmulas de De Moivre: As fórmulas de De Moivre são muito úteis para a potenciação de números complexos. A demonstração abaixo é simples, mas não é a que De Moivre provavelmente fez. Para ver uma demonstração mais provável para a época de De Moivre, clique AQUI e AQUI.
Demonstração: Pela nossa fórmula do corolário acima, a potência do número complexo é igual a:

Mas, como sabemos da propriedade da potência de , temos :


Que é a primeira fórmula de De Moivre. A segunda pode ser obtida através da primeira: é só efetuarmos a substituição . Com isso, temos

Reparem que eu não escrevi logo o que poderia se esperar, ou seja, que . Primeiro, temos que resolver a seguinte equação trigonométrica:

Mas como e , sendo , temos


Obtendo a fórmula

Que é a segunda fórmula de De Moivre.
Corolário 2: O complexo z tem n raízes distintas.
Demonstração: A demonstração está em averiguar que k varia até n-1. Vamos fazer k = n+p, sendo p um número natural maior que zero. Então, a expressão da enésima raiz de z vira

Mas, como sabemos, e , temos

Se p persistir maior que n, podemos reduzir de novo, p = n + q. Daí

Até termos q<n. Ou seja, k varia entre 0 e n-1, formando n possibilidades para a enésima raiz de z.
Corolário 2: As n raízes do número formam um polígono regular de n lados
Demonstração: Como todas as raízes têm o mesmo módulo, então podemos dizer que elas estão dispostas em um círculo. Para mostrar que elas formam um polígono regular, basta provarmos que o ângulo entre duas consecutivas é constante. Então, temos que o argumento de uma raiz é e em uma raiz é , qualquer que seja k. Então, a diferença entre os dois argumentos é

Como e n são constantes, vemos que o ângulo entre os dois módulos das raízes é sempre constante. Então, a corda que é delimitada por duas raízes consecutivas tem sempre a mesma medida de , mostrando que, como os pontos estão sobre uma circunferência e a distância entre dois deles é constante, eles formam um polígono de ângulo interno .

Bem, por hoje é só! Se você gostou do blog, inscreva por e-mail e no blog para receber as novas atualizações e curta nossa página no Facebook. Todas essas opções se encontram na barra lateral do blog e abaixo da postagem. Para melhorar a qualidade de nossas postagens avalie o conteúdo aqui embaixo. É rapidinho! Lembre-se que todo tipo de comentário que respeitar as regras é bem vindo.

Até mais!