Os números complexos, já abordados nesse blog, são um assunto muito abrangente da matemática. O objetivo desse post é enumerar apenas algumas das propriedades menos conhecidas dos números complexos, que podemos utilizar em diversos problemas. Para saber das principais propriedades dos números complexos, e sobre um pouco da história deste conjunto de números, clique aqui e aqui.
Enfim, estas fórmulas aqui apresentadas não foram utilizadas anteriormente por causa do panorama de vista em relação aos complexos ser mais amplo e geral, e não particular e específico, como aqui abordado.
Proposição 2:
Onde |x| denota o módulo do complexo x, e Re(x), a parte real do complexo x.
Demonstração:
Chamando
Temos
Mas,
Cuja parte real é ac+bd, o que completa a demonstração. Notando que a segunda fórmula é apenas uma mudança de sinais da primeira, obtemos, por analogia, a mesma.
Exemplo 1:
Ache todos os números complexos z tais que
Resolução:
Utilizando nossa fórmula na segunda igualdade,
Logo, temos
Ou seja,
Ou
Assim,
Exemplo 2:
Sejam números complexos tais que
e
Resolução:
Então, jogando na nossa outra fórmula,
Logo,
Proposição 2: (Desigualdade triangular para números complexos)
Sejam z, w números complexos. Então
Demonstração: De acordo com a proposição 1,
Então basta provarmos que
Que segue diretamente de
A demonstração de
É apenas uma adaptação da anterior. Então, provaremos apenas que
Usando o mesmo artifício anterior,
Então, basta mostrar que
Que já fizemos.
De fato, este resultado pode ser generalizado: Tomemos n complexos . Podemos provar o resultado de que
Esta demonstração será deixada como exercício ao leitor.
Exemplo 3:
(Croácia) Determine os valores mínimo e máximo, caso existam, da expressão
Resolução:
Para este exercício, precisaremos de uma outra propriedade dos números complexos:
Com isso,
Então,
Utilizando a desigualdade triangular,
Que completa o problema.
Proposição 3:
Demonstração:
I)
II)
Como queríamos demonstrar.
Exemplo 4:
(IME-2012) Dados que são raízes da unidade, calcule
Resolução:
Pelo enunciado,
Então
Elevando à sexta potência,
Que liquida o problema.
Exemplo 5:
(Croácia) Calcule
Resolução:
Primeiro, sabemos que
Então, reduzimo-nos a calcular
Utilizando uma das fórmulas,
Que é a resposta que desejamos.
Agora que já terminamos com nossa seção de propriedades não-triviais dos números complexos, que tal alguns problemas para utilizar, além da capacidade fenomenal do ser humano de pensar, algumas das propriedades já vistas? Os problemas são, além de um treino e um divertimento aos que gostam da matemática, uma maneira boa de aperfeiçoar o pensamento, tanto para vestibulares difíceis quanto para olimpíadas.
Problemas que exigem malícia e raciocínio.
P1.: Escreva na forma trigonométrica o complexo
P2.: Ache todos os complexos tais que
P3.: Resolva
Prove que
P5.: (Croácia) Determine todos os inteiros que satisfazem a igualdade
P6.: (AIME) Uma função f é definida no conjunto dos números complexos por , onde a e b são números positivos. Esta função tem a propriedade de que a imagem de cada ponto no plano complexo é equidistante do ponto e da origem. Dado que
e
, com m e n inteiros positivos primos entre si. Determine m+n.
P7.: (Holanda) A sequência de números complexos é definida por
P8.: Seja uma função e
. Para cada complexo fixo a, prove que há uma única função f tal que

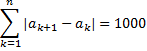
Oi, João!
ResponderExcluirExcelente postagem! Parabéns!
Também dei uma olhada sobre as outras duas de números complexos e são de ótima qualidade.
Abraços!
Olá, Aloisio!
ResponderExcluirMuito obrigado pelo elogio.
Seu blog também não deixa nada a desejar quanto à qualidade, os posts de teoria dos números têm me agradado muito!
Abraços!
Olá, boa tarde!
ResponderExcluirGostaria de ver a solução para o problema P7.