Em geometria, principalmente quando necessitamos provar algo que não envolva, pelo menos diretamente, medida de segmentos, o tema “quadriláteros inscritíveis” é muito útil. Alguns teoremas sobre essa família de quadriláteros são de extrema importância para utilizarmos ângulos que, em muitos casos, se encontram distantes uns dos outros. Em várias ocasiões, encontrar ângulos iguais, triângulos congruentes e semelhantes e quadriláteros inscritíveis são tarefas muito interdependentes: se não conhecemos um teorema sobre um, o outro fica quase impossível.
Portanto, hoje falaremos um pouco das primeiras principais propriedades dos quadriláteros inscritíveis. Definição 1: Um quadrilátero é dito inscritível se seus quatro vértices podem ser colocados sobre uma circunferência.
Agora você pode estar se indagando: mas por que especificamente os quadriláteros inscritíveis? Por que não pentágonos inscritíveis? Ou mesmo triângulos inscritíveis?
Oras, a resposta é bem intuitiva: triângulos são sempre inscritíveis, ou seja, se traçarmos seu circuncentro, podemos construir seu círculo circunscrito. Pentágonos inscritíveis são um quadrilátero inscritível, no qual ligamos um ponto da circunferência aos vértices mais próximos deste, e assim vale para todos os n-ágonos inscritíveis; podemos obtê-los a partir do (n-1)-ágono inscritível. Para tanto, precisamos saber condições para obtermos os quadriláteros inscritíveis, que são, além de tudo, muito mais frequentes que os pentágonos, hexágonos e outros polígonos inscritíveis.
Antes de provarmos nosso teorema principal precisaremos de alguns lemas: Lema 1: Ao traçar uma corda em uma circunferência, todos os segmentos que enxergam a corda em um mesmo semiplano determinado por esta formam o mesmo ângulo.
Demonstração: É o nosso teorema sobre Arco-Capaz, já demonstrado aqui.
Lema 2: Dois pontos, de semiplanos diferentes de uma corda e em uma circunferência, somados, originam um ângulo de 180 graus.
Demonstração: Decorre imediatamente de que, também demonstrado anteriormente, os ângulos que enxergam uma corda ou têm medida C/2 ou 180-C/2, onde C é o ângulo pelo qual o centro enxerga a corda.
Teorema Principal Sobre Quadriláteros Inscritíveis:
I) Todo quadrilátero é inscritível se, e somente se, a soma de seus ângulos opostos é 180 graus. II) Todo quadrilátero é inscritível se, e somente se, ao traçarmos as diagonais do quadrilátero, obtemos que segmentos que enxergam lados iguais têm medidas iguais.
Demonstração:
I) A “ida” é igual à demonstração do Lema 1.
II) A “ida” é igual à demonstração do Lema 2.
Deixarei a “volta” como exercício aos leitores.
Agora, as perguntas podem surgir: Tudo muito bem, tudo muito bom, mas o que isso tem a ver comigo?
Eu respondo: tudo! Oras, quadriláteros inscritíveis matam diversos problemas de diversas olimpíadas e vestibulares de nível IME/ITA. Então, acho que estou prometendo muito e não fazendo nada. Portanto, vou agora resolver alguns problemas relacionados.
Problema 1: (Olimpíada de Mayo – 2009) Seja ABCD um quadrilátero convexo, com ABD sendo um triângulo equilátero e BCD sendo isósceles, com C=90º. Se E é o ponto médio do lado AD,determine a medida do ângulo CED.
Resolução: Tracemos, primeiro, a figura:

Queremos descobrir o ângulo amarelo. Reparemos, inicialmente, que BE é perpendicular a AD, pois ABD é isósceles. Portanto, vemos que o quadrilátero BEDC é inscritível, pois BCD+BED= 90+90=180. Logo, usando o teorema que fala das diagonais, temos que CED=CBD=45º.
Observação: O resultado é independente do triângulo ABD ser equilátero, pois a mesma propriedade é válida para um triângulo isósceles qualquer; Na verdade, a única complicação desse exercício é traçar BE, e enxergar o quadrilátero inscritível, ao que, com o tempo, não é complicação, e sim automático.
Problema 2: (Olimpíada de Mayo – 2010) Considere o retângulo ABCD e a circunferência de centro D e raio DA, que corta o prolongamento do lado AD no ponto P. A reta PC corta a circunferência no ponto Q e o prolongamento do lado AB no ponto R. Demonstre que QB=BR.
Resolução: Considere a figura: 
Reparemos que, por congruência de triângulos retângulos,
Assim,
Como
Assim,
Mas, novamente por congruência de triângulos retângulos,
Problema 3: (IME-1997/Teorema de Miquel para quadriláteros completos) Sejam quatro retas em posição geral, como na figura abaixo. Prove que os circuncírculos dos quatro triângulos formados se encontram em um único ponto (denominado ponto de Miquel).
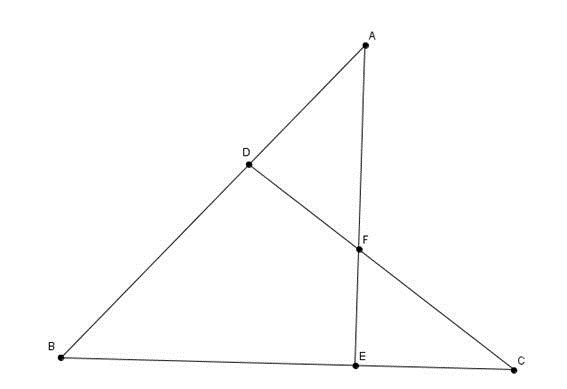
Resolução: Refaçamos a figura, com os respectivos circuncírculos tracejados:

Temos apenas que provar que os quadriláteros BAME e BDMC são inscritíveis. Ora, isso é muito fácil de ver, pois  (FMCE é inscritível) e
(FMCE é inscritível) e  (DAMF inscritível). Logo,
(DAMF inscritível). Logo,  , o que prova para BDMC. Agora, para o quadrilátero BAME, apenas temos de usar um argumento análogo, que será deixado ao leitor.
, o que prova para BDMC. Agora, para o quadrilátero BAME, apenas temos de usar um argumento análogo, que será deixado ao leitor.
Problemas Propostos
Proposto 1: (São Petersburgo-1996) Seja ABC um triângulo tal que BAC=60º. Seja também O um ponto no interior de ABC para o qual AOB = BOC = 120º. Se D,E são os pontos médios dos lados AB, AC, prove que A,D,E,O são cocíclicos.
Proposto 2: (Irlanda 1997) Dado um ponto M interior ao triângulo equilátero ABC, sejam D,E,F os pés das perpendiculares traçadas de M aos lados BC, CA e AB, respectivamente. Encontre o lugar geométrico dos pontos M para os quais FDE=90º.
Proposto 3: Seja P o centro do quadrado construído externamente sobre a hipotenusa AC do triângulo retângulo ABC. Prove que BP bissecta o ângulo ABC.
Proposto 4: (IMO-2002) Sejam S uma circunferência de centro O, BC um diâmetro de S, A um ponto sobre S tal que AOB<120º e D o ponto médio do arco AB que não contém C.Se a reta paralela DA passando por O intersecta AC em I e a mediatriz de OA intersecta S em E e F, prove que I é o incentro do triângulo CEF.
Proposto 5: Seja ABC um triângulo de circuncentro O e ortocentro H tal que BAC=60º e AB>AC. Sejam também BE, CF as alturas relativas aos lados CA, AB, respectivamente, e M,N os pontos sobre os segmentos BH,HF,respectivamente, tais que BM=CN. Determine o valor de:
Bom, pessoal, é tudo por enquanto. Mais tarde teremos outros problemas, e mais teoremas sobre quadriláteros inscritíveis virão, aguardem pelo próximo post.
Se você gostou do blog, inscreva por e-mail e no blog para receber as novas atualizações e curta nossa página no Facebook. Todas essas opções se encontram na barra lateral do blog e abaixo da postagem. Para melhorar a qualidade de nossas postagens avalie o conteúdo aqui embaixo. É rapidinho! Lembre-se que todo tipo de comentário que respeitar as regras é bem vindo.
Até mais!
excelente material...parabéns
ResponderExcluirMuito obrigado pelo elogio.
ExcluirEspero que visite nosso blog mais vezes.
Até mais,
Eduardo.