Brahmagupta (589-668) foi um matemático e astrônomo indiano, e sua principal contribuição, pelo menos àqueles que estudam geometria mais a fundo, é o teorema sobre quadriláteros cíclicos que leva seu nome. Seu teorema é muito importante no cálculo de áreas, inclusive de triângulos. Agora é o momento que você para e pensa: Quadriláteros inscritíveis? Triângulos? Áreas? Calma, vocês verão que tudo vai se acertar. Caso não conheça muito sobre o assunto “quadriláteros inscritíveis”, clique aqui e aqui para saber mais sobre este tópico de geometria plana.
Bom, vamos investigar qual a área de um quadrilátero cíclico, ou inscritível, como queira.
Primeiro, lembremos do nosso primeiro post sobre quadriláteros inscritíveis:
“Um Quadrilátero é inscritível se, e somente se, a soma de ângulos opostos é 180 graus”
Pra que isso vai ser útil? Tudo! Denotemos por ângulos opostos em um quadriláteros cíclico α e γ. Bom, se os lados forem, nessa ordem, a,b,c,d, com o ângulo entre a,b sendo α e γ o ângulo entre c,d. Logo, pela lei dos cossenos nos dois triângulos (eles têm um lado em comum, que é a diagonal):
Utilizando o teorema dos senos para as áreas,
Pois . Assim, utilizaremos o cosseno do ângulo para determinar seu seno. Portanto,
Definindo , e substituindo o seno na fórmula (*), teremos
Notemos também que a famosa fórmula de Heron (ou Herão) de Alexandria é apenas um caso particular da fórmula de Brahmagupta: se tornarmos d=0 (D=C), teremos
Que é válida para todo triângulo, pois todo triângulo é inscritível.
Com essas belas e utilíssimas fórmulas em mãos, podemos resolver muitos problemas. Um deles é o seguinte:
Problema 1: Um quadrilátero é dito bicêntrico quando este é inscritível e circunscritível. Prove que a área máxima de um quadrilátero bicêntro com perímetro fixo ocorre quando as duas circunferências são concêntricas.
Resolução: Ora, pela fórmula de Brahmagupta, temos
Mas, pela condição deste ser circunscritível,
Logo, a área do quadrilátero é
Logo, pela desigualdade entre as médias para quatro números reais positivos,
E a área máxima ocorre se, e somente se, a=b=c=d. Logo, o quadrilátero que queremos é um quadrado. Porém, um quadrado tem ambas circunferências, a circunferência inscrita e a circunscrita, com centro no encontro de suas diagonais, que completa o problema.
Note que esse último problema utilizou argumentos mistos algébricos e geométricos. Isso é muito comum ao se usar a fórmula com a qual estamos trabalhando: geometria “com contas”. Geralmente este termo é utilizado pejorativamente pelos fãs de geometria euclidiana plana, porém não deveria, pois muitos problemas saem muito mais rapidamente quando utilizamos as famosas contas.
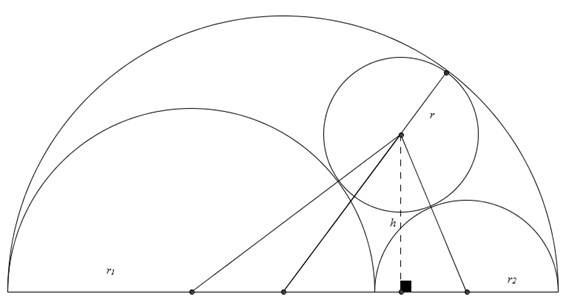
Problema 2: Seja a figura abaixo. Mostre que h=2r.
Resolução: Vale fazer a ressalva que essa estrutura (formada por um semi-círculo maior tangente a dois outros tangentes externamente e internos ao primeiro) é muito conhecida há muito tempo. Seu nome é arbelos, do grego “faca de sapateiro”.
Neste problema, utilizaremos um teorema que ainda não vimos neste blog: o teorema de Stewart. Para saber mais sobre este teorema, clique aqui. Enfim, ele diz que, dado um triângulo como na figura, devemos ter
Depois demonstraremos, pela boa e velha trigonometria, esta importante fórmula. Porém, agora apenas nos convém utilizá-la. Utilizaremo-na no triângulo cuja altura é h e tem vértices nos centros das circunferências internas à maior. Este triângulo tem lados
Considerando a ceviana que liga o centro da circunferência inscrita ao centro da circunferência grande, esta tem medida
E n,m valem, respectivamente
Logo, ao utilizar Stewart, devemos ter
Após algumas (muitas, mas por abreviação deixaremos esta parte ao leitor) manipulações algébricas, conseguimos mostrar que
Agora que entra Brahmagupta (ou quase). Na verdade, é Herão que usaremos aqui, mas já mostramos que Herão é apenas um caso particular de Brahmagupta. Pela fórmula de Herão,
É a área do triângulo. Mas, por outro lado,
Assim, substituindo nossa expressão do valor de r na equação de Herão,
Que nos dá
De onde o resultado segue.
Há muitas outras utilizações destas incríveis expressões de cálculo de área somente em função dos lados dos polígonos. Vale a pena ressalvar que não é possível, caso o quadrilátero não seja cíclico, expressar sua área apenas como função dos lados, e demonstraremos este fato em breve, no próximo post sobre relações de áreas.
Por hoje é só, pessoal. Espero que tenham gostado e que a importância destas fórmula esteja evidenciada após esse post.
Lembre-se: Você está convidado a comentar no blog! Sua opinião, desde que bem-educada, é também bem-vinda! Não se esqueça também de colocar sua opinião nas caixinhas abaixo. É rápido, não leva nem 3 segundos!




Oi, João Pedro!
ResponderExcluirMuito belo e elegante os problemas e resoluções aqui apresentados.
O conhecimento geométrico acumulado pelos antigos é impressionante. Creio que seriam necessários vários tomos para condicioná-los.
Continue nos brindando com estes excelentes posts.
Só uma sugestão. Assim como eu, acho que nossos leitores ficam curiosos de saber a fonte de suas pesquisas.
Um grande abraço.
Muito bom o post e como o Aloisio, também fiquei curioso com as fontes. Continue divulgando matemática de qualidade. Parabéns!
ResponderExcluirOlá, pessoal! Muito obrigado pelos elogios, tentamos sempre passar o conhecimento que temos!
ResponderExcluirQuanto às fontes, peço desculpas por não colocá-las.
Tirei a ideia de demonstração de Brahmagupta do livro do T. Andreescu e Z. Feng, "103 Trigonometry Problems: From the trainning of the USA IMO team".
O primeiro problema eu mesmo elaborei, e o segundo vi em um site que não me lembro, mas é muito conhecido este resultado, acredito até que Arquimedes já soubesse.
Além disso, o teorema de Stewart se deve ao blog parceiro, "O Baricentro da Mente".
vc poderiam colocar as fontes e falar sobre as biografias e contribuiçoes cientificas de hiparco de niceia, brahmagupta, por exemplo, para nos leitores entendermos melhor so a historia e desenvolvimento da trigonometria
ResponderExcluirSHOWWWWWW!!!!!
ResponderExcluirJoão, excelente... Usei as informações para o meu TCC (profmat) .... Muito obrigado
ResponderExcluir