Os Números complexos compõem um assunto muito abordado durante o Ensino Médio. Entretanto, pela experiência, vemos que, nos cursos comuns de Ensino Médio, o tema é abordado superficialmente e muitas das propriedades destes são deixadas de lado. Este é o post de número quatro da série de Números Complexos. Na verdade, este deveria ser o terceiro post, mas vi que havia urgência maior de postar sobre algumas propriedades menos óbvias dos números complexos.
Comecemos com algumas das propriedades mais óbvias, daquelas que conhecemos na escola ao estudar o tema.
Lema 1: Seja z um número complexo e seu conjugado. Temos que
Para todos os polinômios P com coeficientes reais.
Demonstração: Seja
Então
Como queríamos. Note que nesta demonstração apenas usamos as propriedades dos conjugados de um número complexo. Para saber mais sobre propriedades dos números complexos, clique aqui, aqui e aqui.
Com este Lema, obtemos o seguinte
Corolário 1: Se um complexo é raiz de um polinômio de coeficientes reais P, então seu conjugado também é.
Demonstração:
Pode parecer um simples corolário, mas ele será de extrema importância para todo tipo de progresso com relação a complexos e polinômios.
Teorema (Fundamental da Álgebra): Todo polinômio de grau n tem, se contas as multiplicidades separadamente, n raízes complexas. Ou seja, podemos fatorar o polinômio em polinômios de grau um separados.
Demonstraremos este teorema mais tarde aqui no blog, pois um post à parte será destinado a isso. Enquanto isso, veremos a
Versão Real para o Teorema Fundamental da Álgebra: Todo polinômio com coeficientes reais admite fatoração como polinômios do grau 1 ou 2 com coeficientes reais.
Demonstração: Se considerarmos, juntamente, nosso corolário e o teorema fundamental da álgebra, podemos fatorar o polinômio como:
Onde ri são as raízes reais de P, e as demais são raízes complexas. Ora, podemos, então agrupar os fatores
Mas ambos são reais (verifique), o que completa a demonstração.
Façamos uma ressalva: nem nosso corolário nem esta versão para o Teorema Fundamental da Álgebra são válidas para polinômios com coeficientes complexos. Estes têm particularidades que não nos convém estudar neste momento, pois aqueles com coeficientes reais são muito mais comuns em problemas e provas, como veremos.
Agora, temos de reparar sobre algo importante: raízes da unidade. Raízes da unidade de ordem n são números complexos que, elevados a n, dão 1. Por isso raízes da unidade! Mas o que elas têm de tão importantes em polinômios? Ora, tudo! Alguns problemas são liquidados quase que instantaneamente ao utilizarmos bem uma raiz da unidade. Por isso, vejamos um aspecto incrível sobre estes números complexos:
Proposição 1: O polinômio 1 + x + x2 + x3 + ... + xn-1 admite todas as raízes n-ésimas da unidade distintas de 1. No mais, é possível conseguir um polinômio com coeficientes reais que admita as raízes n-ésimas de um número real positivo a distintas da própria raiz real.
Demonstração: Lembremos que a fórmula de uma progressão geométrica de razão x e primeiro termo 1 é
Logo, ao substituir qualquer complexo da forma ζ=cis 2kπ/n na fórmula, obteremos que seu numerador é zero e seu denominador é claramente distinto de zero. Porém, ao substituir 1 na fórmula do lado direito, obtemos denominador zero. Agora, substituindo no lado esquerdo, obtemos valor n que, claramente, não é uma raiz. Logo, temos que este polinômio admite todas as raízes n-ésimas de 1 que não são 1. Reparem que este resultado implica no importante
Corolário 1:
Demonstração: Repare que estas condições equivalem às relações de Girard. Pelo próprio polinômio, temos o desejado.
Antes de avançar aos exercícios resolvidos, temos de ver um importante
Teorema 2: Se r é um raiz de multiplicidade m de um polinômio P, então ela é uma raiz de multiplicidade m-1 da sua derivada, e de m-2 de sua derivada segunda, assim por diante. (Por definição, se r for raiz de multiplicidade 0 de algum polinômio, r não é raiz do polinômio).
Demonstração: Pelo enunciado,
Onde Q(r)≠0. Utilizando as propriedades das derivadas,
Substituindo r em mQ(x) + Q’(x)(x-r), obtemos mQ(r)≠0. Assim, temos que mQ(x) + Q’(x)(x-r) não admite r como raiz, que completa a demonstração. Para demonstrar para as derivadas subsequentes, apenas temos que aplicar este processo o quanto quisermos.
Enfim, vamos a alguns exercícios resolvidos:
Problema 1: Sejam P,Q,R,S polinômios satisfazendo
Prove que (x-1) é um fator de P.
Resolução: A substituição óbvia a fazer seria x=1. Porém, ao substituirmos, ela não nos dá, pelo menos aparentemente, nada de proveitoso. Ao reparar no “coeficiente” do polinômio S, reparamos a malandragem do problema: substituir por todas as raízes quintas da unidade! Logo, obteremos o sistema
Logo, somando, obteremos
Logo,
Que implica que
Então, substituindo nas fórmulas,
Que completa a demonstração.
Problema 2: Ache uma fórmula fechada para
Resolução: Seja . Então, pela terceira aula sobre complexos:
Com isso, elevando o complexo à n-ésima potência, temos, pelo binômio de Newton,
Queremos, portanto, a parte real desta soma. Porém, pela igualdade da terceira aula,
Que é a fórmula que desejamos.
Fiquem ligados no blog para exercícios sobre este assunto e outras postagens interessantes, e não se esqueça de avaliar o post aqui embaixo. É rapidinho!


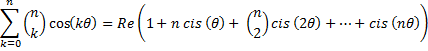
Comentários
Postar um comentário
Você pode comentar! A equipe do blog encoraja todos a comentar.
Porém, lembre-se que comentários que desrespeitem as regras abaixo serão excluídos:
-É proibido ofender qualquer pessoa ou grupo em seu comentário.
-Os comentários deverão ser minimamente relacionados com o tópico. Lembrem-se, estamos falando de um blog de matemática!
-Proibido flood.
-Proibido palavras de baixo calão.
-Proibido colocar qualquer tipo de conteúdo improprio para menores de 18 anos (há menores de idade que acessam o blog).
A equipe do blog agradece seu comentário, e tenha certeza que será muito enriquecedor. Tentaremos respondê-los o quanto antes possível.