Esse post é exclusivo para a resolução de problemas. Resolvi fazer isso, pois a resolução de problemas pode ser muito grande e tomar muito tempo, então colocá-la junto ao post de quadriláteros inscritíveis faria que esse post fosse muito grande, e de difícil compreensão. Com esse post, inauguramos a seção de “geometria em problemas”, que é muito útil, pois acho que geometria é basicamente constituída de problemas, e os teoremas apenas nos dão a base para a imaginação.
Nosso primeiro problema foi da prova da OBM de 2011. Antes de começarmos, entretanto, vejamos alguns dos teoremas usados na resolução.
Teorema 1: A bissetriz interna em um triângulo ABC , digamos, partindo do ponto A até o ponto K, nos fornece relações de proporcionalidade baseadas em
Demonstração: Seja a figura abaixo:
Utilizando a lei dos senos no triângulo BAK,
Agora, utilizando a lei dos senos no triângulo CAK,
Logo,
De onde seguem as relações.
Teorema 2: Os teoremas sobre quadriláteros inscritíveis, que vocês podem conferir aqui.
Bom, com os teoremas em dia, podemos partir para o enunciado em si.
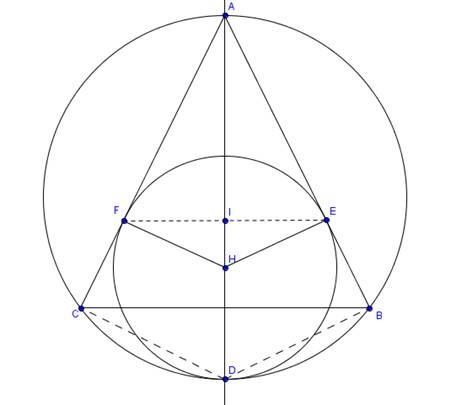
Problema 5 – OBM 2011: Seja ABC um triângulo acutângulo e H seu ortocentro.As retas BH e CH cortam AC e AB em D e E, respectivamente. O circuncírculo de ADE corta o circuncírculo de ABC em F diferente de A. Provar que as bissetrizes internas de BFC e BHC se cortam em um ponto sobre o segmento BC.
Demonstração: A figura do problema:
Primeiro, reparemos que a condição do problema equivale a provar que a razão dada pelo teorema da bissetriz interna nos triângulos BFC e BHC seja igual. Portanto, devemos ter
Notemos, primeiramente, que FBCA é inscrito. Logo, BFC=α. Notemos também que BCDE é inscritível, pois BEC=BDC=90º. Logo, BCE=BDE=90-β. Assim, ADE=90-(90-β)=β. Portanto, obtemos que o triângulo ADE é semelhante ao triângulo ABC. Assim, por F estar inscrito na circunferência de ADE, AFE=180-β. Analogamente, por F estar na circunferência de ABC, AFB=180-γ, o que faz BFE=180-γ-(180-β) = β-γ.
Olhando, agora, para o quadrilátero EAFD, vemos que este é inscrito, de modo que BFC=BAC=α, assim como FBCA é inscrito, de modo que BFC = BAC = α. Como BFC e EFD têm valores iguais, e o ângulo EFC é comum, CFD = BFE = β-γ. Agora, FEHD é inscritível. Assim, EFH=EDH=90-β. Somando a BFE e a HFC, temos HFC +(β-γ) + (90-β) = α, o que faz HFC = 90 – β = EFH.
Porém, o triângulo BFE é semelhante ao triângulo CFD, pois BFE = CFD e FBE = FCA. Do mesmo modo, BHE e DHC são semelhantes. Botando em razões de semelhança,
Mas, pela segunda semelhança,
O que nos dá
Por outro lado, notemos que o triângulo BFC é semelhante ao triângulo EFD, pois BFC=EFC, e FBC = 180-FAC=FED. Botando, mas uma vez, em razões de semelhança,
De onde obtemos que
Que nos mostra que as bissetrizes internas de BFC e BHC se intersectam em um ponto sobre BC, que conclui a prova.
Agora, vamos ao segundo problema, que eu vi em um simulado para a IMO de 2010. Não existe um teorema específico para resolver, somente que as três bissetrizes de um triângulo se encontram em um ponto (o incentro), mas isso acho que todos nós sabemos. Então, ao enunciado:
Problema do Simulado da IMO: No triângulo ABC, os pontos D,E são pertencem ao interior do lado AC tais que ABD=DBE. O ponto F pertence ao segmento BD e é tal que CF é perpendicular a BD. O ponto P pertence ao segmento BE e é tal que APF = BPF . Prove que CFP = FAP.
Resolução: Seja a figura do problema:
Se chamarmos DBE=α, e BPF=β, obtemos BFP= 180-(α+β). Logo, CFP = 90-(α+β). Por outro lado, reparemos que F é incentro do triângulo ABP, pois é o encontro das bissetrizes de APB e ABP. Logo, FAP=BAF. Como BAP = 180-(2α+2β), então FAP = 90-(α+β), de onde decorre a relação do enunciado.
Avante ao terceiro problema. É o problema 4 da IMO de 1978, e para resolvê-lo teremos de usar um Lema que será demonstrado durante o mesmo. Sem mais delongas, o enunciado:
Problema 4 da IMO de 1978: Em um triângulo ABC nós temos AB=AC. Um círculo é tangente internamente ao circuncírculo de ABC e também aos lados AB,AC, em E,F, respectivamente. Prove que o ponto médio de EF é o centro do círculo inscrito em ABC.
Resolução: Como em todo problema de geometria, uma boa figura pode nos render problemas dificílimos. Porém, antes, provaremos um poderosíssimo lema que praticamente transformará o problema em aplicação de trigonometria. “Mas que lema importante é esse?”, você pode estar a se perguntar. Para não enrolar mais, aqui vai:
Lema: Seja o circuncírculo de um triângulo ABC. O incentro do triângulo é equidistante do ponto médio de qualquer um dos (menores) arcos definidos por dois quaisquer pontos do triângulo.
Demonstração: Façamos a demonstração para um arco qualquer, sendo os outros análogos. À figura, como sempre:
Chamemos, por simplicidade de notação, BAC=α, ABC=β,ACB=γ. Como o quadrilátero ABDC é inscrito, temos BDI=γ, e DBC = α/2. Como CBI= β/2, temos BID = 180 – (β/2 + α/2 + γ) = β+α-(β/2 + α/2) = β/2 + α/2, que mostra que BDI é um triângulo isósceles. O mesmo pode ser feito (deixo como exercício aos leitores) para o triângulo CDI.
Com o nosso lema em mãos, podemos utilizá-lo livremente na resolução do problema.
Comecemos “deslocando” o objetivo da prova: pelo lema, temos apenas que provar que BD=DC=DI. Assim, o modo que escolhi para demonstrar esse problema é bem trigonométrico, e veremos que dá certo. Chamemos, por facilidade de notação, CAD=x. Pela condição do enunciado, HE é perpendicular a AB, assim como HF é perpendicular a AC. Repare que isto nos dá AHE = 90-x. Logo, pela congruência entre os triângulo AFH e AHE, FHE=180-2x. Repare também que isto nos mostra que o quadrilátero AFHE é inscritível, assim, FEH = x. Pelo ponto médio de uma corda ser perpendicular ao centro, ao chamarmos o raio da circunferência menor r, teremos
Agora, pela semelhança de triângulos AHE e ADB, temos, chamando DB=y,
Como CD=DB, temos apenas que mostrar que
Portanto, o ponto médio de EF é realmente o incentro do triângulo.
Bem, a todos que leram esse artigo, espero que tenham entendido todas as resoluções. Fiz como um tipo de continuação do post sobre quadriláteros inscritíveis, pois em dois dos três problemas os quadriláteros inscritíveis são muito importantes, e em outro uma propriedade básica é muito útil. Enfim, caso não tenham entendido, sintam-se livres para comentar, que eu ou o meu parceiro de blog Eduardo respondemos, e avaliem também o post aqui embaixo, para que nós saibamos como estamos nos saindo didaticamente/em questão de conteúdo.




alert(‘Aopa!’);
ResponderExcluirOlá, é possível resolver esse problema sem usar trigonometria?
ResponderExcluirobrigado.