Desculpem-me pelo atraso, mas só consegui escrever esta seção de problemas nesse momento. Então, comecemos pelos novos enunciados.
Teoria dos Números
1 – (IMO-1979) Sejam p,q naturais tais que
Prove que p é divisível por 1979.
2 – Em uma circunferência de círculo, são colocados os 1000 primeiros naturais. Começamos a marcar a partir do 1, e de 15 em 15. O processo acaba quando marcamos algum número que já foi marcado. Quantos números, ao final, serão deixados sem marca?
Álgebra
3 – (IMO-1975) Seja e
. Prove que
4 – (IMO-1973) Ache o mínimo de , onde a equação
Tem pelo menos uma raiz real.
5 – Sejam as raízes diferentes de um de
Prove que
Geometria
6 – (IMO-1975) Nos lados de um triângulo arbitrário ABC, os triângulos BPC, CQA e ARB são construídos externamente satisfazendo
Combinatória
7 – (OIbM-2010) Existem inteiros positivos a,b tais que a sequência definida por x1=2010, x2=2011,
Contenha apenas números inteiros?
8 – Divide-se um círculo em quatro setores de mesma área, através de cordas que passam por seu centro. Dispomos de k cores para pintá-lo, de modo que cada região tenha uma cor diferente das duas adjacentes. Qual o menor valor de k para qual isso é possível? Existe uma fórmula fechada pro número de maneiras? Se sim, dê esta fórmula.
Agora, resolvamos alguns dos problemas anteriores, presentes aqui:
2 – A resposta é não. Se a poligonal é fechada, então, se uma reta passa por segmentos mas não vértices, ela passa por um número par de segmentos. Logo, não pode passar por todos os segmentos.
5 – Notemos que podemos escrever
Mas, isso se torna óbvio, pois, como φ é injetiva, e o domínio é igual à imagem, esta é também é sobrejetiva, concluindo que esta é uma bijeção do domínio nele mesmo. Se ela é uma bijeção, pode ser vista como uma permutação do domínio. Agora fica fácil: só temos que utilizar a desigualdade das permutações. Como temos uma sequência bem ordenada (1<2<...<k<...<n), assim como a sequência dos inversos dos quadrados desses inteiros é inversamente ordenada, a permutação que nos dá o valor máximo é que associa cada termo de cada sequência ao seu relativo ordenado na outra sequência, e a que dá o valor mínimo é a que associa cada termo ao seu termo oposto em ordem de grandeza. Ora, o termo oposto em ordem de grandeza da primeira sequência é o inverso de seu quadrado (verifique você mesmo). Logo, a permutação do lado direito é a que nos dá o menor valor possível. Qualquer outra nos dará um valor maior, que prova nossa desigualdade.
7 – Utilizaremos um princípio do qual falarei sobre no blog: o Princípio das Casas dos Pombos, ou Princípio das Gavetas de Dirichlet. Para ver mais sobre esse princípio no blog parceiro Fatos Matemáticos, clique aqui e aqui.
Enfim, Consideremos os números 2008, 20082008, 200820082008,..., 2008...2008 (no último número, 2008 aparece n vezes). Pelo princípio das casas dos pombos, temos n-1 restos diferentes de 0 na divisão por n. Bom, temos n números, o que nos dá que pelo menos dois deles têm o mesmo resto divididos por n. Então, ao fazer a diferença dos dois, teremos um número que começa por 2008 e é múltiplo de n, que completa a prova.
Os outros problemas não resolvidos ficam de dever de casa ao leitor. Para os que querem enviar problemas para a próxima seção/soluções aos problemas apresentados, podem escrever para joaopedroblogger@hotmail.com.
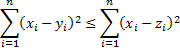
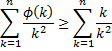
Comentários
Postar um comentário
Você pode comentar! A equipe do blog encoraja todos a comentar.
Porém, lembre-se que comentários que desrespeitem as regras abaixo serão excluídos:
-É proibido ofender qualquer pessoa ou grupo em seu comentário.
-Os comentários deverão ser minimamente relacionados com o tópico. Lembrem-se, estamos falando de um blog de matemática!
-Proibido flood.
-Proibido palavras de baixo calão.
-Proibido colocar qualquer tipo de conteúdo improprio para menores de 18 anos (há menores de idade que acessam o blog).
A equipe do blog agradece seu comentário, e tenha certeza que será muito enriquecedor. Tentaremos respondê-los o quanto antes possível.