Como contar usando Bijeções

Olá! Nessa postagem falarei sobre bijeções, que em análise combinatória é apenas mais uma forma de contar o número de elementos de um conjunto. Para um bom entendimento dessa postagem, será preciso que você domine o que foi falado nessa postagem aqui.

Inicialmente eu gostaria de deixar claro o que é uma bijeção, ou função bijetora. 

Dados dois conjuntos A e B, uma função 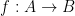 é qualquer lei que diz como associar cada um dos elementos de "A" a somente 1 elemento de B. 

Uma função pode ser Injetora, Sobrejetora, ou Bijetora.

Uma função [; f: A \rightarrow B ;] é Injetora quando satisfaz a condição abaixo:

 , . 

Observe que numa função injetiva, com os conjuntos A e B finitos, a imagem de f tem o mesmo número de elementos que o domínio

Uma função  [; f: A \rightarrow B ;]  é Sobrejetora quando satisfaz a condição abaixo:

De forma simplificada

Uma função é Bijetora quando é ao mesmo tempo Injetora e Sobrejetora. 

Assim, uma função é Bijetora se todo elemento de A está associado a exatamente 1 elemento de B e

se todo elemento de B for associado a algum elemento de A. 

Não é difícil de notar que a definição acima implica, para A e B conjuntos finitos, que A e B tem a mesma cardinalidade (mesmo número de elementos). E implica também, para A e B quaisquer que toda função Bijetora possui uma função inversa. E por essas propriedade ela é tão útil para a análise combinatória.

Antes de fazer qualquer comentário vamos ver um exemplo.

Como colocar 6 pessoas diferentes em 3 filas de banco que estão organizadas como na imagem ao lado?


Repare que a ordem em que as pessoas estão em cada uma das filas é importante, bem como a fila em que elas ocupam.

Para contar isso, vamos fazer uma bijeção entre os casos possíveis e alguma outra situação mais simples de contar.

!!!Chamarei de "desenho da fila" o desenho que expressa uma possível disposição dessas 6 pessoas nessas filas. !!!


Entre cada fila há 1 espaço vazio. Vamos denota-los com uma |.

Se do inicio até o final da fila estiverem as pessoas A, B, C e D, nessa ordem, representaremos como ABCD; defina o inicio da fila como o lugar mais próximo da onde se encontram os atendentes.
Assim, se na primeira fila, estiverem as pessoas do inicio até o final estiverem as pessoas A, B, C e D. Depois na segunda fila estiver a pessoa E e na terceira a pessoa F, a combinação que seria associada a esse desenho da fila seria: ABCD | E | F

Ou seja:

equivale a (ABCD | E | F ) e vice-versa.







Assim como a combinação (DEFACB||) equivale a colocar as 6 pessoas na
 primeira fila, colocando do inicio até o final as pessoas D, E, F, A, C e B nessa ordem. Ou seja, (DEFACB||) equivale ao desenho da fila ao lado.





Acho que já ficou claro que qualquer que seja o desenho dado, existe uma e somente uma combinação dos elementos "A", "B", "C", "D", "E", "F", "|" e "|" que equivale a aquele desenho, assim como dada qualquer combinação desses elementos existe somente um desenho da fila que está associado a essa combinação.  Isso faz com que a lei que transforma os desenhos das possíveis filas em combinações seja uma bijeção. Ora, se é uma bijeção com conjuntos que possuam um número finito de elementos, então o número de filas é igual ao número de combinações. E, convenhamos, é mais fácil contar o número de combinações.

Isso é uma permutação com 8 elementos sendo 2 deles idênticos, logo, o número de filas  é: .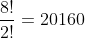

Uma coisa a se observar é que a dificuldade do problema acima foi mostrar que de fato a função que transformava os desenhos em combinações era de fato uma bijeção. No caso, todo desenho podia ser obtido se você soubesse em que ordem as pessoas estão organizadas em suas respectivas filas?
Observe que essa característica estava muito bem definida nas combinações.

(IME) Uma rua possui um estacionamento em fila com N vagas demarcadas junto ao meio-fio de um dos lados. N automóveis, numerados de 1 a N, devem ser acomodados, sucessivamente, pela ordem numérica no estacionamento. Cada carro deve justapor-se a um carro já estacionado, ou seja, uma vez estacionado o carro 1 em qualquer uma das vagas, os seguintes vão se colocando imediatamente à frente do carro mais avançado ou atrás do carro mais recuado. Quantas configurações distintas podem ser obtidas desta maneira.

Observe que ao estacionar o carro 1 define quantas pessoas estacionaram à frente e quantas estacionaram atrás dele.  Para definir uma combinação você precisa de 2 informações sobre ela:

1- Quais carros pararam atrás do carro 1 e em que ordem pararam.
2- Quais carros pararam à frente do carro 1 e em que ordem pararam.

Bem, como os carros são acomodados sucessivamente pela ordem numérica, é razoável pensar que ao informar onde cada carro que chega para  (à frente ou atrás da fila) estamos definindo a fila inteira.

Vamos por exemplo mostrar como funcionaria com 5 carros.
Se após todos pararem a fila estivesse assim:
(5,2,1,3,4) então podemos representa-la assim: (frente, atrás,atrás,frente).
Observe que: (frente, atrás,atrás,frente) indica que o carro 2 parou à frente do carro 1, que o carro 3 parou atrás do carro 1, que o carro 4 parou atrás da fila e que o carro 5 parou à frente da fila. E que a posição do carro 1 também está definida já que são 5 vagas e há 2 carros atrás dele ele está na posição do meio. Ou seja, a posição de todos os carros foi bem definida.

Para resolver esse problema, resta:

*Definir a lei que associa cada combinação a uma sequência de palavras "frente" e "atrás".
*Mostrar que essa associação é uma bijeção encontrando a inversa dela.
*Calcular o número de sequências formadas pelas palavras "frente" e "atrás".

A lei que associa cada sequência será a seguinte:

**Em ordem, cada palavra será associada a escolha de cada carro, sendo a primeira palavra associada a escolha do segundo carro e a n-ésima palavra relacionada a escolha do (n+1)-ésimo carro. Assim, a posição de cada carro estará bem definida em relação a posição inicial do primeiro carro. Repare que se o primeiro carro estiver ocupando a k-ésima vaga, então haverão k-1 palavras "atrás" e n-k palavras "frente".

Para encontrar a inversa dessa função, é só ver que dada uma sequência das palavras "frente" e "atrás" é possível encontrar uma única combinação que é associada a ela.

Para isso, se há k palavras "atrás", então o carro de número 1 ocupa a k+1-ésima vaga. Após marcar a vaga ocupada pelo carro 1, vai-se preenchendo em ordem as posições dos outros carros.

Ex: (frente, atrás, frente, frente). Observe que há 1 palavra atrás, ou seja, o carro de número 1 ocupa a segunda vaga. Logo, temos inicialmente (-,-,-,1,-), ao ler a primeira palavra da sequência a combinação passa a ser (-,-,2,1,-), ao ler a segunda palavra da sequência a combinação passa a ser (-,-,2,1,3), ao ler a terceira palavra da sequência a combinação passa a ser (-,4,2,1,3) e ao ler a última palavra a combinação passa a ser (5,4,2,1,3).

Bem, acho que já ficou bem claro que é uma bijeção. Agora basta contar o número de sequências. Que é dado por . Como é uma bijeção, o número de configurações distintas que podem ser obtidas com N carros é .

Eu sei que não fui muito direto na resolução dos dois problemas acima. Foi proposital, pois eu queria deixar bem claro como aplicar essa técnica. Vamos ver como fica resolvendo de formas mais direta.

1- (OBM) Quantos números inteiros positivos entre 10 e 1000 possuem seus dígitos em ordem estritamente crescente? (Por exemplo, 47 e 126 são números desse tipo; 52 e 566 não).

Como não precisamos nos preocupar com o 1000, vamos considerar 2 grupos, números de 10 a 99 e números de 100 a 999.  Repare que os algarismos deveram ser distintos, e que ao escolher dois algarismos distintos existe somente um número desse tipo que pode ser formado usando eles.

Bijeção clara entre os números possíveis e a escolha de dois algarismos distintos. Isso por que dado um número possível só há 1 escolha de dois algarismos que pode forma-lo, e dados dois algarismos distintos só há 1 número desse tipo que pode ser formado usando esse algarismo.

Análogo para 3 algarismos.

Assim concluímos que existem tantos números de 10 a 99 quanto números de formas de escolher dois algarismos distintos e que existem tantos números de 100 a 1000 quanto números de formas de escolher 3 algarismos distintos.

Resposta: .

2- Seja P(n) o número de maneiras de expressar n como uma soma de inteiros positivos, e P(n,m) o número de maneiras de expressar n como a soma de exatamente m inteiros positivos. Prove que P(n)= P(2n,n).

Vamos definir P'(n,m) como o número de maneiras de expressar n como uma soma de exatamente m números que podem ser inteiros positivos ou zeros. Assim P'(2,2)= 2. Que são 1 + 1 e 0+2. Observe que P(n)=P'(n,n). Isso por que se escrevermos

 então é só acrescentar  zeros que ele se tornara um dos casos que são contados em P'(n,n). Observe que essa lei é inversível, dado um dos casos que é contado em P'(n,n) é só retirar todos os zeros da soma para obter um correspondente em P(n).

Assim basta mostrar P'(n,n)=P(2n,n). O que é fácil. Observe que P(2n,n) é o número de maneiras de expressar 2n como a soma de n inteiros positivos, ou seja, são maiores ou iguais a 1. Logo, vamos supor  que todos são 1. Para a soma totalizar 2n falta somar n, ou seja, distribuir n uns entre os n números existentes, sendo que algum(ns) número(s) pode(m) receber nenhum  1 e algum(ns) pode(m) receber mais que um 1. Ou seja, P(2n,n) é igual ao número de formas de escrever n como uma soma de exatamente n números, que podem ser  inteiros positivos ou zeros. Em outras palavras P(2n,n)=P'(n,n). C.Q.D.

Observe que no problema acima, foi usado bijeção não para contar, mas para garantir, por exemplo, que P'(n,n)=P(n). 

Problemas propostos. Agora que você já leu bastante sobre esse método que tal praticar?

1- (OBM) Esmeralda, a digitadora, tentou digitar um número de seis algarismos, mas os dois algarismos 1 não apareceram (a tecla devia estar com defeito). O que apareceu foi 2004. Quantos são os números de seis algarismos que ela pode tentar digitar?

2- (OBM) Definimos o diâmetro de um subconjunto não vazio de {1,2,3,...,n} como a diferença entre seu maior elemento e seu menor elemento (em módulo).

Calcule a soma dos diâmetros de todos os subconjuntos não vazios de {1,2,3,...,n}.

3- (OBM - ALTERADA)Quantos números de 4 algarismos tem seus algarismos, em ordem, crescentes? (por exemplo 1234 e 1122 são números desse tipo; 5321 e 5332 não).

Por hoje é só! Se você gostou do blog, divulgue para seus amigos nas redes sociais, curta nossa página no facebook logo ao lado e se inscreva por e-mail e no blogger para receber nossas atualizações. Não se esqueça de avaliar o conteúdo de nossas postagens logo abaixo, não demora nada e é muito importante para sabermos a qualidade do que escrevemos. Você também pode comentar a vontade, deixando sua crítica, sugestão ou elogio. Tentaremos responder o mais rápido possível.

Até mais!

Fontes: 

Apostila distribuída no POTI, curso oferecido no IMPA.  Você pode visualiza-la clicando aqui