Olá, pessoal. Sabemos que ficamos um bom tempo sem postar conteúdo novo no blog, porém estamos buscando, a cada dia, remediar esta situação: postamos, até agora, 7 vezes no mês, e até o final deste feriado prometemos pelo menos mais 3 postagens para quem nos lê com frequência. Como, contudo, escrever muito sobre assuntos requer tempo e revisão, estamos escrevendo sobre problemas e técnicas separadamente, só que aprofundamo-nos na medida do possível em assuntos interessantes, para que o leitor interessado não deixe de se divertir.
Foi pensando nisso que criamos a seção de problemas: problemas nós temos à vontade e à nossa disposição sempre que quisermos, não é necessário criar problemas somente nossos para postá-los (como fazemos com os posts que contém mais conteúdo), e sempre é um desafio a mais para o leitor interessado.
Porém, como devem ter reparado, está perto de completar três meses que não postamos nossa seção de problemas. Até dia primeiro de novembro, o blog andou parado por causa dos estudos de nós, autores. Afinal, certos momentos pedem enfoques em diferentes coisas, como qualquer um deve saber. Entretanto, aquele leitor mais assíduo deve notar que nós não postamos na nossa primeira semana (semana passada).
Muitos podem ter pensado que pararíamos com a seção de problemas semanal, que tudo iria ser abandonado e que, quem sabe, nos contentaríamos com postar apenas pequenos posts sobre assuntos rápidos. Aos fãs, não temam! A seção de problemas está de volta - desta vez, muito melhor! Vamos selecionar 6 problemas para cada área, e adicionaremos, à medida que o tempo correr e que expusermos mais conteúdo no blog, mais e mais áreas, como Cálculo, Álgebra Linear, Análise, etc.
Portanto, está dado o recado. Chega de ladainha, vamos apresentar nossos problemas:
Teoria dos Números
1 - (Olimpíada Mineira de Matemática) Existe um quadrado perfeito que comece com o bloco de dígitos 2012?
2 - Prove que há infinitas soluções inteiras positivas para
3 - Mostre que não existe um triângulo retângulo com lados inteiros tal que sua área seja um quadrado perfeito.
4 - Ache todos os triângulos 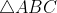 tais que seus lados
tais que seus lados 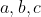 são inteiros e
são inteiros e 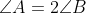 .
.
5 - Encontre todos os inteiros m,n tais que
6 - (Harvard-MIT - 2012 - Novembro) Defina f (n) como o resto de  quando dividido por 23, para cada inteiro positivo n. Determine o menor k tal que f (n + k) = f (n), para todo inteiro positivo n.
quando dividido por 23, para cada inteiro positivo n. Determine o menor k tal que f (n + k) = f (n), para todo inteiro positivo n.
2006+(n-1)}})
Álgebra
1 - Encontre todos os valores possíveis de
2 - (Harvard-MIT - 2011) Seja 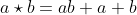 . Determine
. Determine )))) .
.
3 - (Harvard-MIT - 2011 - Fevereiro) Seja, para todo x real,
%20=%20\frac{1}{\sqrt[2011]{1-x^{2011}}})
^k}{x^l}%20-1%20=\frac{(x+1)^m}{x^n})
=\frac{f(x+n)-f(x)}{n})
3 - (Harvard-MIT - 2011 - Fevereiro) Seja, para todo x real,
Ache }(2011)^{2011}) , onde
, onde }(x)%20=%20f(f^{(n-1)}(x))) .
.
4 - Sejam k,l,m,n inteiros não negativos. Encontre todas as quádruplas ordenadas (k , l , m , n) tais que, para todo x diferente de zero,
5 - (Harvard-MIT- 2011) Calcule 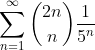 .
.
6 - Ache todos os a racionais tais que }\in%20\mathbb{Q}) .
.
Geometria
1 - Dizemos que dois triângulos são homotéticos se eles são semelhantes e têm lados paralelos. Prove que, dados dois triângulo homotéticos, as retas obtidas pela união dos vértices relativos são concorrentes.
2 - (Olimpíada Mineira de Matemática) Dado um quadrilátero convexo ABCD, seja um ponto M em seu interior. Sejam G1,G2,G3,G4, respectivamente, os baricentros dos triângulos ABM, CMB, DCM, ADM.
(a) Prove que G1G2G3G4 é um paralelogramo.
(b) Qual a razão entre a área de G1G2G3G4 e de ABCD ?
3 - (OMERJ-2011) Sejam ABC um triângulo com AB = AC e D
o pé da bissetriz relativa ao vértice A. Sejam também Γ a circunferência
circunscrita a ABC e P o ponto onde a reta tangente a Γ por A encontra a reta
BC. Finalmente, seja E o ponto de
interseção da bissetriz do ângulo APB com o lado AB. Mostre que DE é paralelo a
AC.
4 - (Ibero) Seja ABC um triângulo equilátero, e Γ sua circunferência inscrita. Prove que, independentemente do ponto que escolhemos sobre Γ, a soma dos quadrados das distâncias deste aos vértices do triângulo é constante.
5 - (Ibero) Um triângulo ABC está inscrito em uma circunferência de centro O. Suas alturas são AD, BE e CF. A reta EF encontra a circunferência em P e Q.
(a) Prove que OA é perpendicular a PQ.
(b) Sendo M ponto médio de BC, prove que AP² = 2.AD.OM.
6 - (OBM-2012) Dado um triângulo ABC, sejam 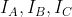 os ex-incentros relativos aos vértices A,B,C, respectivamente. Sejam X,Y,Z os pontos médios de
os ex-incentros relativos aos vértices A,B,C, respectivamente. Sejam X,Y,Z os pontos médios de 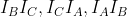 , respectivamente. O incírculo de ABC toca os lados BC, CA e AB em D, E, F, respectivamente. Prove que DX, EY, FZ concorrem em um ponto da reta IO, onde I e O são o incírculo e o circuncírculo de ABC, respectivamente.
, respectivamente. O incírculo de ABC toca os lados BC, CA e AB em D, E, F, respectivamente. Prove que DX, EY, FZ concorrem em um ponto da reta IO, onde I e O são o incírculo e o circuncírculo de ABC, respectivamente.
Combinatória
1 - (Harvard-MIT - 2012 - Novembro - Guts exam) Yuhang faz braceletes. Quantos braceletes distintos pode ele fazer com 6 contas, se ele têm 2 contas verdes, duas azuis e duas vermelhas? Braceletes que podem ser obtidos através de reflexão ou rotação devem ser considerados iguais.
2 - (Desafio PUC-Rio de Matemática) Três urnas são colocadas uma ao lado da outra contra uma parede. Em cada urna há inicialmente quatro bolas vermelhas e quatro bolas azuis.
O jogador, que sempre está de frente para a parede, começa em frente à urna do meio e retira de lá uma bola (as bolas são retiradas ao acaso e depois de examinadas são descartadas). Se a bola for vermelha, o jogador se move para a esquerda. Se a bola for azul, ele se move para a direita. Ele retira, novamente ao acaso, uma bola da urna que se encontra à sua frente. Novamente, se a bola for vermelha, ele se move para a esquerda; se for azul, ele se move para a direita. O jogador repete ao processo até o jogo terminar, o que ocorre se o jogador receber uma ordem impossível (tirar uma bola vermelha na urna da esquerda ou uma azul na urna da direita) ou se ele esvaziar as bolas em uma das urnas.
Qual a probabilidade de que aconteça este último caso, ou seja, de que o jogador esvazie uma das urnas antes do jogo acabar?
3 - (Harvard-MIT - 2012 - Novembro - Team exam) Seja uma permutação dos números de 1 a 2012. Calcule a probabilidade de que
uma permutação dos números de 1 a 2012. Calcule a probabilidade de que )%20=%202012) .
.
4 - Seja) o número de partições de n, e
o número de partições de n, e ) o número de partições de n com tamanho m. Prove que
o número de partições de n com tamanho m. Prove que %20=%20p(n)) .
.
(Obs.: uma partição de um número é uma maneira de escrevê-lo como soma de outros números)
5 - (W.L. Putnam Maths Competition - 2010) Para todo inteiro n, qual o maior k tal que podemos colocar os inteiros de 1 a n em k caixas de modo que a soma dos números em cada caixa é igual?
6 - (Desafio PUC-Rio de Matemática-2012) Temos um tabuleiro 8x8 e peças 1x3 (triminós retos). Queremos, com os triminós, cobrir 63 das casas do tabuleiro, deixando 1 restante. Para quais casas do tabuleiro que não serão cobertas essa cobertura é possível?
2 - (Desafio PUC-Rio de Matemática) Três urnas são colocadas uma ao lado da outra contra uma parede. Em cada urna há inicialmente quatro bolas vermelhas e quatro bolas azuis.
O jogador, que sempre está de frente para a parede, começa em frente à urna do meio e retira de lá uma bola (as bolas são retiradas ao acaso e depois de examinadas são descartadas). Se a bola for vermelha, o jogador se move para a esquerda. Se a bola for azul, ele se move para a direita. Ele retira, novamente ao acaso, uma bola da urna que se encontra à sua frente. Novamente, se a bola for vermelha, ele se move para a esquerda; se for azul, ele se move para a direita. O jogador repete ao processo até o jogo terminar, o que ocorre se o jogador receber uma ordem impossível (tirar uma bola vermelha na urna da esquerda ou uma azul na urna da direita) ou se ele esvaziar as bolas em uma das urnas.
Qual a probabilidade de que aconteça este último caso, ou seja, de que o jogador esvazie uma das urnas antes do jogo acabar?
3 - (Harvard-MIT - 2012 - Novembro - Team exam) Seja
4 - Seja
(Obs.: uma partição de um número é uma maneira de escrevê-lo como soma de outros números)
5 - (W.L. Putnam Maths Competition - 2010) Para todo inteiro n, qual o maior k tal que podemos colocar os inteiros de 1 a n em k caixas de modo que a soma dos números em cada caixa é igual?
6 - (Desafio PUC-Rio de Matemática-2012) Temos um tabuleiro 8x8 e peças 1x3 (triminós retos). Queremos, com os triminós, cobrir 63 das casas do tabuleiro, deixando 1 restante. Para quais casas do tabuleiro que não serão cobertas essa cobertura é possível?
Cálculo*
1 - (W. L. Putnam Maths Competition - 2010) Encontre todas as funções f dos reais nos reais, tais que
Para todo x real e n inteiro.
3 - (Harvard-MIT 2011) Calcule ^{2011}%20dx) .
.
3 - (Harvard-MIT 2011) Seja f [0,1] 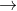 [0,1] uma função satisfazendo f ( f(x)) = 1, para todo x contido no domínio. Determine o conjunto de todos os valores possíveis de
[0,1] uma função satisfazendo f ( f(x)) = 1, para todo x contido no domínio. Determine o conjunto de todos os valores possíveis de dx) .
.
*A seção de Cálculo terá menos problemas nesta primeira edição, como qualquer categoria que entrar na seção de problemas. Se deve à introdução de uma categoria, pois levamos em conta se ela fará sucesso ou não.
Fiquem ligados no blog para mais e mais postagens. Se você leu, gostou e aprovou, comente abaixo! Temos também um sistema de avaliação de post, onde em um click apenas você dá sua opinião. Vamos, não custa nada!
Comentários
Postar um comentário
Você pode comentar! A equipe do blog encoraja todos a comentar.
Porém, lembre-se que comentários que desrespeitem as regras abaixo serão excluídos:
-É proibido ofender qualquer pessoa ou grupo em seu comentário.
-Os comentários deverão ser minimamente relacionados com o tópico. Lembrem-se, estamos falando de um blog de matemática!
-Proibido flood.
-Proibido palavras de baixo calão.
-Proibido colocar qualquer tipo de conteúdo improprio para menores de 18 anos (há menores de idade que acessam o blog).
A equipe do blog agradece seu comentário, e tenha certeza que será muito enriquecedor. Tentaremos respondê-los o quanto antes possível.