Hoje vamos ter nossa seção de problemas de número 8. Chegamos até aqui com muitos problemas já propostos, com níveis de dificuldade crescente e, em maioria, interessantíssimos. Nesta edição, não vai ser diferente: problemas extremamente interessantes, mais uma vez. Portanto, o leitor interessado ganha sempre. Comecemos logo:
Teoria dos Números
1 - (OBM-1993) Seja a sequência definida por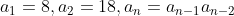 
. Determine todos os n tais que 
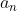é quadrado perfeito.
2 - (OBM-1992) Prove que existe n tal que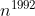 
começa com 1992 uns.
3 - Dada uma sequência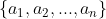
de inteiros positivos, prove que existe k natural tal que 
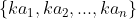contém apenas potências perfeitas.
4 - (Simulado POTI) Existe_{k\in\mathbb{N}})
uma sequência de números inteiros tal que todas as sequências _{k\in\mathbb{N}})
contém apenas um número finito de primos, para todo a natural?
5 - Prove que existem infinitos n naturais tais que a equação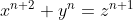
tem solução nos inteiros não-nulos.
6 - Ache todos os n tais que}-1}{n})
é um quadrado perfeito.
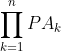
3 - Dada uma sequência
4 - (Simulado POTI) Existe
5 - Prove que existem infinitos n naturais tais que a equação
6 - Ache todos os n tais que
Álgebra
1 - (OBM-1989) Seja f: Z em Z tal que f (x) = x -10 para todo x > 100, e f (f (x + 11)), para x menor ou igual a 100. Determine o conjunto de todos os valores assumidos por f.
2 - Definimos, para todo n natural, a n-ésima soma harmônica como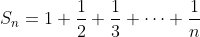 
. Prove que:
(a) À medida que n tende a infinito, Sn tende a infinito.
(b) }%20\le%20S_n%20\le%20\ln{n}+1)
3 - Dada uma circunferência unitária e um polígono regular de n lados inscrito nesta, ache o conjunto dos pontos P que maximizam o produto
4 - (AIME-1997) Dados u,w raízes distintas da equação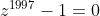 
, ache a probabilidade de 
.
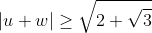5 - (Polônia - 2011) Ache todos os pares de funções f,g: R em R tais que
f(y)=g(x)g(y)+g(x)+g(y),%20\forall%20x,y\in\mathbb{R})
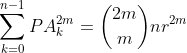
Combinatória
\le%20\sum_{k=1}^{n}%20d(n)\le%20n\left%20(1%20+%20\frac{1}{2}+\frac{1}{3}+\cdots%20+%20\frac{1}{n}%20\right%20))
4 - Sejam A,B,C tais que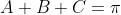
. Prove que
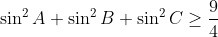
6 - Dada uma circunferência de raio r e um polígono regular A0A1...An-1 de n lados inscrito nesta, prove que, para qualquer ponto P tomado na circunferência e um natural m < n,
Combinatória
1 - (OBM-1992) Seja d(n) o número de divisores de n. Prove que
2 - Em um país há N cidades, e de cada uma partem 4 estradas de mão dupla. Sabe-se que pode-se ir de uma estrada a qualquer outra por meio das estradas. Prove que, mesmo retirando uma estrada, podemos ir de uma cidade a qualquer outra por meio das estradas.
3 - Um grafo é um conjunto (V,E) de vértices e arestas (falaremos mais de grafos depois), onde dois vértices são ligados ou não por uma aresta. Um grafo é conexo se podemos ir de um vértice deste a qualquer outro por meio das arestas. Definimos )
como o maior número de vértices do grafo conexo G que podemos retirar deste para assegurar que este continue conexo. Definimos )
analogamente, só que em relação as arestas.
(a) Um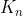 
é o grafo de n vértices onde cada vértice é conectado a todos os outros. Determine ,%20\lambda(G))
para este grafo.
(b) Um grafo é bipartido quando podemos separá-lo em 2 classes de vértices: quaisquer dois vértices dentro de cada classe não são adjacentes (ou seja, não há uma aresta conectando dois vértices em uma mesma classe). Um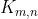 
é um grafo bipartido em que as classes têm m e n vértices cada e, ao selecionar um vértice de uma classe, este é adjacente a todos os vértices da outra classe. Determine para este grafo.
(c) Um cubo d-dimensional é um grafo no conjunto dos vértices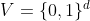 
, ou seja, do conjunto das sequências )
onde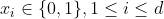 
, onde é ligada uma aresta se, e somente se, dois vértices diferem em apenas uma posição na sequência. Determine para este grafo.
4 - Aline está no ponto (0,0) de uma malha de pontos inteiros, e Bianca está no ponto (m,n) da mesma malha, de coordenadas inteiras positivas. Aline só pode andar para cima e para o lado direito, e Bianca só pode andar para baixo e para a esquerda. Ambas fazem um movimento por segundo, onde um movimento consiste de se mover uma unidade para uma das direções permitidas.
(a) Determine todas as duplas m,n para as quais existe um percurso de Aline e Bianca tal que estas se encontram.
(b) Para tais duplas, calcule a probabilidade de que este encontro ocorra.
5 - (IMO-1982) Seja )
a média aritmética dos mínimos de todos os subconjuntos de r elementos de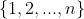 
. Mostre que %20=%20\frac{n+1}{r+1})
.
6 - Temos n moedas viciadas, onde a probabilidade de se obter uma cara na k-ésima moeda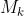 
é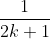 
. Ao jogarmos todas as n moedas exatamente uma vez, qual a probabilidade de obtermos um número ímpar de caras?
Geometria
1 - (Ásia-Pacífico 2012) Seja P um ponto no interior do triângulo ABC, e sejam D,E,F os pontos de interseção de AP com BC, de BP com CA e de CP com AB, respectivamente. Prove que a área de ABC é 6 se a área de PFA,PDB e PEC é 1.
2 - (IMO) Em um triângulo ABC, a bissetriz do ângulo BCA intersecta o círculo circunscrito do triângulo ABC novamente no ponto R, a mediatriz de BC em P, a mediatriz de AC em Q. O ponto médio de BC é K e o ponto médio de AC é L. Prove que os triângulos RPK e RQL têm a mesma área.
3 - Seja P um ponto no interior do triângulo ABC, e sejam D,E,F os simétricos de P em relação aos lados BC,AC,AB, respectivamente. Qual a maior área, do triângulo ABC ou do triângulo DEF?
2 - (IMO) Em um triângulo ABC, a bissetriz do ângulo BCA intersecta o círculo circunscrito do triângulo ABC novamente no ponto R, a mediatriz de BC em P, a mediatriz de AC em Q. O ponto médio de BC é K e o ponto médio de AC é L. Prove que os triângulos RPK e RQL têm a mesma área.
3 - Seja P um ponto no interior do triângulo ABC, e sejam D,E,F os simétricos de P em relação aos lados BC,AC,AB, respectivamente. Qual a maior área, do triângulo ABC ou do triângulo DEF?
4 - Sejam A,B,C tais que
5 - (TST-Brasil) Seja K uma circunferência de centro O tangente aos lados AB e AC do triângulo ABC nos pontos E e F, respectivamente. A reta perpendicular a BC através de O intersecta o segmento EF em D. Prove que A,D e M (ponto médio do lado BC) são colineares.
6 - (USAMO - 2008) Um reticulado (m,n) é o espaço eucidiano de todos os pontos com coordenadas m,n inteiras. Pergunta-se: é possível cobrir todos os pontos do reticulado com discos de raio ao menos 5, sem superposição de discos?
Bom, é tudo pelo mês! Se você gostou do blog, siga-nos no Facebook, por email ou no blog para receber nossas atualizações. Para contatar a equipe do blog, em caso de dúvidas, sugestões ou soluções aos problemas, envie um e-mail para amatematicapura@hotmail.com. Além disso, convidamos todos a comentarem! É rápido, melhoramos o sistema de comentários para que todos possam postar à vontade. Por último, não se esqueçam de avaliar a postagem, aqui embaixo. É rapidinho, não custa nada!
Ótima publicação... Me chamo Romirys Cavalcante e gostaria muito de fazer parceria com seu blog... O que acha ??? A propósito hoje eu fiz uma publicação em meu blog e marquei o seu blog nela... O que acha de visitar ela pra comentar se possível??? Se quiser irei deixar aki em anexo o link para essa postagem... Espero que aceite o pedido de parceria e que visite a postagem em que divulguei seu blog ^^
ResponderExcluirhttp://romirys.blogspot.com.br/2012/12/fui-tagueado.html
olá gostei desse blog por que é uma maneira de aprendizado pra muita gente, gostaria de ser mais um parceiro desse blog o meu blog é o "link matemático"
ResponderExcluirhttp://linkmatematico2013.blogspot.com
Olá, Murilo!
ExcluirNa nossa barra lateral há uma caixa com as orientações para fazer parceria conosco. Lembre-se que nosso e-mail mudou recentemente para "amatematicapuraoficial@gmail.com", assim, se você já havia mandado o seu banner para o e-mail antigo, mande novamente para o e-mail atual.
Até mais,
A Matemática Pura.
Este comentário foi removido pelo autor.
ResponderExcluir