Hoje vamos falar
de um dos conceitos primordiais da teoria de Equações Funcionais, que é a
equação de Cauchy. De fato, a Equação de Cauchy generaliza o conceito de operador linear: Se T for um operador linear definido na
reta com valores reais, então 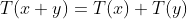 , além de
, além de 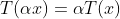 .
.
Diremos que uma função 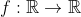 é aditiva se ela satisfaz a primeira condição para ser um operador linear, ou seja, se
é aditiva se ela satisfaz a primeira condição para ser um operador linear, ou seja, se  . A esta condição chamaremos condição de Cauchy ou Equação Funcional de Cauchy, ou simplesmente Equação de Cauchy.
. A esta condição chamaremos condição de Cauchy ou Equação Funcional de Cauchy, ou simplesmente Equação de Cauchy.
As soluções desta equação são muito interessantes, pois é (muito) fácil ver que 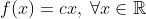 é uma solução, onde c é uma constante. Podemos nos indagar se esta não é a única solução de tal equação. Como veremos adiante, surpreendentemente, isto é falso, e por isso é tão interessante e tao rica a teoria das equações de Cauchy definidas na reta. Mas antes, vamos provar nosso resultado mais básico:
é uma solução, onde c é uma constante. Podemos nos indagar se esta não é a única solução de tal equação. Como veremos adiante, surpreendentemente, isto é falso, e por isso é tão interessante e tao rica a teoria das equações de Cauchy definidas na reta. Mas antes, vamos provar nosso resultado mais básico:
Proposição 0: Seja f uma função aditiva. Então f é Q-linear, ou seja, f (qx) = qf (x), para todo q racional e todo x real. Em particular, f (q) = q f (1) para todo q racional.
Demonstração: Da aditividade, vemos que
Em particular, para n = m e x = y/m, então
Fazendo y = nz acima, obtemos
Terminando a prova da Q-linearidade. 
Proposição 1: Seja f aditiva, que não se anula identicamente, e que é também multiplicativa, ou seja, 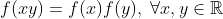 . Então f (x) = x para todo x real.
. Então f (x) = x para todo x real.
Demonstração: Da multiplicatividade, vemos que f (1) = 1. Como f é Q-linear, então f (q) = q, para todo racional. Basta vermos que f é crescente: De fato, se f for crescente, como Q é denso na reta, então
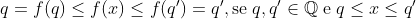
Assim, vemos que

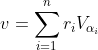

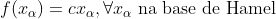
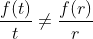
Como epsilon foi arbitrário, então f (x) é maior ou igual a x. De modo análogo, f (x) é menor ou igual a x.
Mas é óbvio que f é crescente: pela aditividade, basta mostrar que f é positiva para positivos, o que sai do fato que f (x²) = f (x)².
Logo, f (x) = x, para todo x real, como desejávamos. 
Até agora, só vimos exemplos de como as coisas podem dar certo quando falamos de equação de Cauchy. Como veremos a seguir, soluções podem ser muito mais estranhas - e em geral são, se assumirmos o Axioma da Escolha. Motivados por isso, vamos relembrar alguns pré-requisitos.
Definição:Uma base para um espaço vetorial (sobre um corpo K) é um conjunto 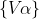 tal que, para qualquer v no espaço vetorial, existem
tal que, para qualquer v no espaço vetorial, existem 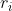 em K com
em K com
Fato: Todo espaço vetorial tem uma base (uma prova desse fato, que utiliza o lema de Zorn - equivalente ao Axioma da escolha -, pode ser encontrada aqui).
Portanto, consideremos a reta R como um espaço vetorial sobre Q. Assim, existe uma Base de Hamel para a reta sobre Q, desde que assumamos o Axioma da Escolha. Logo, seja 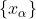 uma tal base, e tome uma g função definida em tal conjunto com valores reais. Definindo
uma tal base, e tome uma g função definida em tal conjunto com valores reais. Definindo
Então vemos facilmente pela definição de base que f é aditiva, e, por construção, definida em todos os reais. Vê-se (exercício) que f só é contínua se existir c real com
Basta, então, tomar uma f definida na base que não satisfaça tal propriedade, e obteremos uma solução descontínua para a Equação de Cauchy. Nossos próximos dois resultados nos mostram o quão patológicas são as soluções não-contínuas da Equação de Cauchy:
Teorema 2: Se f é solução não-contínua da Equação de Cauchy, então o conjunto (x, f (x)) (gráfico de f ) é um subconjunto denso de R².
Demonstração: Dado t em R, da condição de descontinuidade, então existe um r real tal que
Isto significa, porém, que 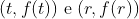 formam uma base para R² (pois são Linearmente independentes). Logo, seu span é o R² inteiro. Portanto, Q.(t, f (t)) + Q.(r, f (r)) é um conjunto denso no R², e tal conjunto (pela Proposição 0) está no gráfico da f, que conclui a demonstração.
formam uma base para R² (pois são Linearmente independentes). Logo, seu span é o R² inteiro. Portanto, Q.(t, f (t)) + Q.(r, f (r)) é um conjunto denso no R², e tal conjunto (pela Proposição 0) está no gráfico da f, que conclui a demonstração. 
Corolário 3: Dado qualquer intervalo I de medida positiva (pode ser aberto, fechado, semi-aberto em qualquer direção), então a imagem deste intervalo por uma solução descontínua da Equação de Cauchy é densa na reta.
Demonstração: Suponha que não; Portanto, existiria [c,d] intervalo que não tem interseção com f (I). Assim, I x [c,d] não teria interseção com o gráfico de f, contradizendo a densidade deste último em R². 
Agora que sabemos que, de fato, estudar a equação de Cauchy é interessante, seria conveniente saber quando essa equação se torna contínua. A resposta inclui hipóteses absolutamente gerais:
Teorema 4: Uma função aditiva 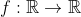 ser contínua é equivalente a
ser contínua é equivalente a
i) f ser limitada (inferior, superior ou ambos) em algum intervalo limitado.
ii) f ser monótona.
iii) f ser localmente integrável.
iv) f ser diferenciável.
v) f (x) = cx para todo x real e algum c.
vi) f ser mensurável em um conjunto C de medida positiva.
vii) f ser limitada (inferior, superior ou ambos) em um conjunto C de medida positiva.
viii) f ser contínua em um ponto dado.
ix) f (x) ser positiva (ou negativa) para todo x positivo.
x) Existir um conjunto C de medida positiva tal que neste conjunto f é limitada por cima por uma g mensurável.
Demonstração: Ver exercício 3 abaixo. 
Terminaremos a parte teórica com um caso particular interessante
Problema (Halperin): Dada uma função f aditiva tal que f (1/x) = f (x)/x², f tem de ser contínua?
Resposta: Sim! A prova, surpreendentemente, é bem simples:
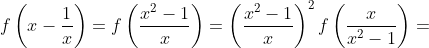



Porém,
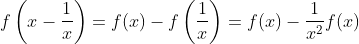
Do que fizemos, então, temos que f (x) = f (1) x, como desejávamos.
Problema (Halperin): Dada uma função f aditiva tal que f (1/x) = f (x)/x², f tem de ser contínua?
Resposta: Sim! A prova, surpreendentemente, é bem simples:
Porém,
Do que fizemos, então, temos que f (x) = f (1) x, como desejávamos.
Exercícios
1 - Prove que todo espaço vetorial tem uma base, usando o Lema de Zorn: "dado um conjunto parcialmente ordenado 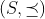 tal que, para todo subconjunto completamente ordenado
tal que, para todo subconjunto completamente ordenado  , este possui uma cota superior
, este possui uma cota superior 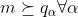 . Então S possui ao menos um elemento maximal M, ou seja,
. Então S possui ao menos um elemento maximal M, ou seja, 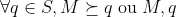 são incomparáveis"
são incomparáveis"
2 - Prove que f (definida numa base de Hamel e estendida de forma aditiva) só é contínua se valer a condição de 'linearidade' na base de Hamel escolhida.
3 - Prove o Teorema 4, demonstrando
a) Que f contínua implica cada uma das afirmações (i)-(x).
b) Por absurdo que f não pode ser descontínua se valerem (i),(ii),(viii) e (ix), estabelecendo, assim, a equivalência com esses itens.
c) Que (iii) e (iv) implicam (vi)
d) Que se f é limitada em um conjunto de medida positiva C, então
(d.1) C + C contém um intervalo. (veja aqui como provar)
(d.2) (vii) implica (i).
e) Que se f é mensurável em um conjunto C de medida positiva, então existe n tal que
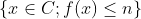
a) Que f contínua implica cada uma das afirmações (i)-(x).
b) Por absurdo que f não pode ser descontínua se valerem (i),(ii),(viii) e (ix), estabelecendo, assim, a equivalência com esses itens.
c) Que (iii) e (iv) implicam (vi)
d) Que se f é limitada em um conjunto de medida positiva C, então
(d.1) C + C contém um intervalo. (veja aqui como provar)
(d.2) (vii) implica (i).
e) Que se f é mensurável em um conjunto C de medida positiva, então existe n tal que
tenha medida positiva. Veja então que (vi) implica (vii).
f) Que se (x) valer, usando a mensurabilidade de g, então vale também (vii).
4 - Ache todas as f : R →R tais que f (x² + f (y)) = y + f (x)², para todos x,y reais.
5 - Seja f : R →R uma função que satisfaz a condição de quase-aditividade seguinte:

f) Que se (x) valer, usando a mensurabilidade de g, então vale também (vii).
4 - Ache todas as f : R →R tais que f (x² + f (y)) = y + f (x)², para todos x,y reais.
5 - Seja f : R →R uma função que satisfaz a condição de quase-aditividade seguinte:
f (x + y)² = (f (x) + f (y))² , para todos x,y em R.
Prove que f é aditiva.
Dicas e Sugestões
1 - Se V é o espaço, considere o conjunto de subconjuntos linearmente independentes de V, munidos da ordem parcial dada pela inclusão.
3 - (a) Sabe-se que f é contínua se, e somente se, é como no item (v). Logo, prove que uma função deste item tem todas essas propriedades.
(b) Use o Teorema 2 e o Corolário 3.
(d) Veja o problema 3(a) do link.
(e) Considere a união de tais conjuntos com n variando nos naturais.
(f) Argumente como em (e), usando g.
4 - Prove que f (0) = 0, f (-x) = - f (x) e que f (x + y) = f (x) + f (y) se x > 0.
5 - Expanda f (x + y + z)² de duas maneiras diferentes.
Referência:
- KANNAPPAN, Pl. Functional Equations and Inequalities with Applications, First Edition. New York, 2009.
Comentários
Postar um comentário
Você pode comentar! A equipe do blog encoraja todos a comentar.
Porém, lembre-se que comentários que desrespeitem as regras abaixo serão excluídos:
-É proibido ofender qualquer pessoa ou grupo em seu comentário.
-Os comentários deverão ser minimamente relacionados com o tópico. Lembrem-se, estamos falando de um blog de matemática!
-Proibido flood.
-Proibido palavras de baixo calão.
-Proibido colocar qualquer tipo de conteúdo improprio para menores de 18 anos (há menores de idade que acessam o blog).
A equipe do blog agradece seu comentário, e tenha certeza que será muito enriquecedor. Tentaremos respondê-los o quanto antes possível.