Oi, pessoal.
Como prometido, vamos mostrar aqui mais alguns problemas interessantes. Relembrando que, aos interessados em ver ou enviar soluções dos problemas anteriores, nos mandem uma mensagem no e-mail amatematicapuraoficial@gmail.com
Problema 1 - Definição: O espectro de um operador linear T (definido num espaço de Banach E com valores em E) é definido como o conjunto dos λ complexos tais que o operador T - λI não é bijetivo.
Seja
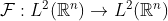
Como prometido, vamos mostrar aqui mais alguns problemas interessantes. Relembrando que, aos interessados em ver ou enviar soluções dos problemas anteriores, nos mandem uma mensagem no e-mail amatematicapuraoficial@gmail.com
Problema 1 - Definição: O espectro de um operador linear T (definido num espaço de Banach E com valores em E) é definido como o conjunto dos λ complexos tais que o operador T - λI não é bijetivo.
Seja
A transformada de Fourier de L² em L². Relembre o teorema de Plancherel: "A transformada de Fourier é um isomorfismo isométrico de L² em L²".
(a) Utilizando este teorema, mostre que, se λ é tal que F - λI não é injetiva, então λ é uma raiz quarta da unidade.
(b) Mais ainda, mostre que o espectro todo está contido no conjunto das raizes quartas da unidade (Dica: fatore 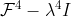 )
)
(c) Mostre que de fato tais pontos estão no espectro da transformada de Fourier
Problema 2 - Relembrando o fato de que uma função que satisfaz a equação de Cauchy e é mensurável é, então, linear (veja aqui), mostre que se f é uma função de R² em R, tal que f (x,y) = g(x)h(y), e, para cada M matriz em O(2) (matrizes 2 por 2 ortonormais), então f (M(x,y)) = f (x,y), com g e h integráveis na reta, com integral 1, então f (x,y) = C exp(-r(x²+y²)), para algum r,C constantes.
Problema 3 - Sejam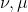 medidas finitas e positivas definidas num espaço X. Suponha que existe
medidas finitas e positivas definidas num espaço X. Suponha que existe 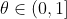 tal que
tal que
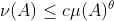
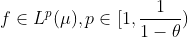
Problema 3 - Sejam
(a) Prove que, se 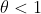 , então, como
, então, como 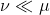 (prove!), mostre que a derivada de Radon-Nikodym
(prove!), mostre que a derivada de Radon-Nikodym
(b) Se 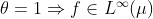 .
.
Problema 4 - Considere uma sequência 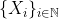 de variáveis aleatórias independentes e igualmente distribuídas, e suponha que
de variáveis aleatórias independentes e igualmente distribuídas, e suponha que

Prove que, então, 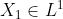 , e use isto para concluir que
, e use isto para concluir que 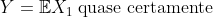 .
.
Problema 5 - (OBM-U 2014 - Primeira fase) Determine todos os pares (n,r) de inteiros positivos tais que existe uma festa com n pessoas onde cada pessoa conhece exatamente r outras (considere que, se uma pessoa A conhece B, então B conhece A).


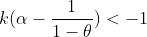

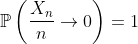
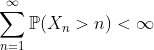
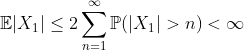
Dicas e Sugestões
Problema 1 - (a) Use o teorema de Plancherel diretamente com a f tal que 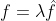 .
.
(b) Suponha que λ não seja uma raiz quarta da unidade. Mostre que, portanto, o operador 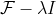 é sobrejetivo, e, para que λ esteja no espectro, temos que a injetividade falha, chegando num absurdo.
é sobrejetivo, e, para que λ esteja no espectro, temos que a injetividade falha, chegando num absurdo.
(c) Considere funções das formas
Onde as constantes são escolhidas de maneira esperta.
Problema 2 - Use a condição de invariância pra obter uma equação de Cauchy com g,h e simplesmente use o problema 3 da seção anterior.
Problema 3 - (a) Escreva
Para k tal que
E use repetidas vezes a desigualdade
(b) Prove que, neste caso, f < 3c quase certamente.
Problema 4 - Usando a convergência quase certa, mostre que
Com isso, mostre, usando o lema de Borel-Cantelli (versão independente) que
E mostre que isso implica que (se X são positivas, é o feito acima; caso contrário, vale o mesmo com módulo)
Para terminar, use a Lei dos Grandes Números (versão Forte ou Fraca).
Problema 5 - Use contagem dupla para ver que nr tem de ser par. Usando indução em n, mostre que tal condição é, de fato, suficiente para que tal festa exista.
Esperamos que vocês gostem desses problemas, e se divirtam com eles. Qualquer sugestão/dúvida, não hesite em nos contactar em amatematicapuraoficial@gmail.com.
Fique ligado para mais posts interessantes sobre matemática.
Comentários
Postar um comentário
Você pode comentar! A equipe do blog encoraja todos a comentar.
Porém, lembre-se que comentários que desrespeitem as regras abaixo serão excluídos:
-É proibido ofender qualquer pessoa ou grupo em seu comentário.
-Os comentários deverão ser minimamente relacionados com o tópico. Lembrem-se, estamos falando de um blog de matemática!
-Proibido flood.
-Proibido palavras de baixo calão.
-Proibido colocar qualquer tipo de conteúdo improprio para menores de 18 anos (há menores de idade que acessam o blog).
A equipe do blog agradece seu comentário, e tenha certeza que será muito enriquecedor. Tentaremos respondê-los o quanto antes possível.