Ok, pessoal, estamos há algum tempo sem postar, então pra quebrar esse jejum separei alguns problemas que achei interessantes. São em nível de IME-ITA. Tente ver a ideia geral por trás de cada solução, elas são muito úteis para resolver problemas mais difíceis. Esperamos ajudar quem deseja treinar para a matemática apresentada nos concursos de tais institutos.
Vamos lá!
1- Quais os últimos três dígitos do quadrado do produto das raízes positivas da equação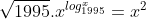 
?
2- Na figura abaixo, o ponto P do menor arco A B dista 6 cm e 1 0 cm , respectivamente, das tangentes
AQ e BQ . Calcule a distância, em cm , do ponto P à corda A B .
3- Para quantos valores reais de p as três raízes de
são números inteiros positivos?
4- Qual o valor de 
, onde u e v são números complexos não nulos satisfazendo 
?
5- Sejam X, Y e Z três números reais maiores que um que satisfazem 
,
então quanto vale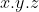 
?
6- Qual é o valor de 
?
Soluções:
1- Esse problema é bastante simples.
Fazendo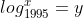 
temos 
Se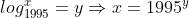 
sendo 
e 
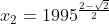então
Logo, os 3 últimos dígitos do quadrado do produto das raízes da equação são 995.
Dica: Quando estiver trabalhando com logaritmos tenha sempre em mente que log é uma função injetora.
Ou seja, log a = log b então a = b. Em demonstrações mais rigorosas vale a pena observar essa propriedade antes de usá-la (apenas escrever algo do tipo: "como log é uma função injetora, temos... ").
2-
Bem, vamos primeiro fazer uma figura com as informações que temos.
Sendo C, E e D as projeções de P sobre os lados AQ, AB e BQ do triângulo respectivamente temos:
#
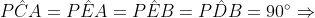PDBE e PCAE são quadriláteros inscritíveis. Logo,
Além disso, traçando os segmentos OA e OP vemos que OAP é um triângulo isósceles. Assim,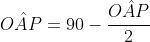 
e como 
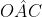= 90º temos que 
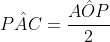. E das propriedades de arco capaz, 
.
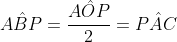Assim,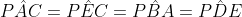 
. Analogamente 
.
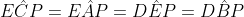Assim,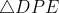 
.
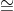
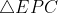
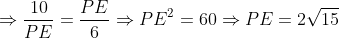A dica é lembrar da relação entre CÂP e AÔP essa relação costuma ser esquecida.
3- Observe que 1 é raiz da equação independente do valor de p. (sempre vale a pena checar por algumas raízes triviais. Tente números como 1, 2, -1, -2 ... )
Assim, usando o método de Briot-Ruffini podemos fatorar da seguinte forma:
Assim, sendo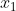 
e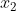 
as raízes da da equação temos: 
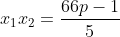e 
.
Ao somar e adicionar 1 para tentar fatorar como 
não conseguirá muita coisa.
Por sorte (ou será que não?) 
, o que facilita a conta. Assim, podemos substituir p por 
.
Temos:
Assim,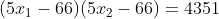 
. Os divisores de 4351 são 1, 19, 229 e 4351. Assim, montamos a seguinte tabela.
Valor possível de
|
Valor de
|
Valor de
|
Valor de
|
Valor de
|
(Não é inteiro)
|
(Não é inteiro)
|
|||
Observe que para cada valor possível de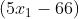 
existe apenas um valor de 
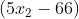tal que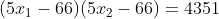
Observe também que se fizermos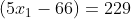 
obteremos os mesmos valores d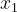e 
e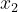 
trocados, como nos interessa apenas quantos valores possíveis de P fazem as raízes serem inteiras positivas isso não faz diferença.
Além disso, não foram considerados os divisores negativos porque nesses casos, ao examinar, vê-se que não conseguiremos ambos, 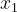e 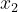, positivos.
Assim, só há um valor de p que faz 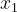e 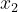serem inteiros positivos, que é p = 76.
A ideia principal de problemas desse tipo é procurar uma fatoração do tipo (aX + b)(cY-d) = E e analisar caso a caso lembrando que os números são inteiros (nem sempre se exige que eles sejam positivos)
4- Observe que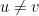 
caso contrário 
e os números são não nulos.
Assim, multiplicando por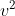 
e dividindo por 
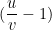, que é diferente de zero, temos:
Onde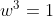 
Assim,
5 - Se 
então
Observe que 
como 
temos 
.
Agindo de forma análoga pra Y e Z temos:
Logo,
Analogamente temos 
e 
. Assim,
6- Vejamos, primeiro, quanto vale 
.
Pela fórmula do binômio de Newton temos:
Observe que para p par temos que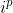 
é real. Assim, com p = 2n temos
Assim, equivale a parte real de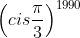 
.
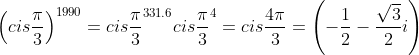logo, a parte real é 
.
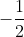A dica desse tipo de questão é tentar procurar um binômio de Newton que se pareça com a expressão procurada. No geral os fatores envolvidos no somatório podem dar dicas, mas ainda é preciso alguma criatividade. Eu tinha um professor que dizia que "Na primeira vez é mágica; a partir da segunda é técnica".
Bem, por hoje é só. Se você gostou do blog curta nossa página no facebook e se inscreva por e-mail para receber nossas atualizações. Não se esqueça de avaliar a postagem logo abaixo, é muito importante sabermos a qualidade do que estamos produzindo.
Até mais.
Caro Dudu, na solução do 1º problema, acho que você cometeu um equívoco: quando você multiplicou x1 por x2 (duas potências de mesma base), você multiplicou os expoentes, quando deveria tê-los somado. Você obteve x1.x2 = 1995^1/2. O correto seria x1.x2 = 1995^2. Estou certo? Grato, Edson (edson.zuit@hotmail.com).
ResponderExcluir