Matemática Através de Problemas - III

Depois de uma longa interrupção, retornamos com mais problemas! 

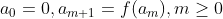
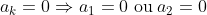
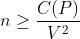
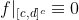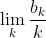
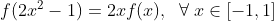
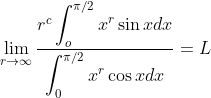
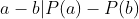
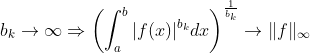
1 - (Putnam) Seja f polinômio em Z[x], e defina 

Mostre que, se existir k tal que 

2 - (Putnam) Seja P um poliedro. Mostre que existe uma constante C(P) > 0 tal que, se uma coleção de n bolas, cuja soma dos volumes é V, cobre a superfície de P, então 

3 - Chamamos uma sequência crescente de números reais positivos 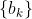 de sequência limite absoluto se, dado um intervalo [a,b] e uma função f contínua tal que existe um intervalo [c,d] com a < c < d < b com 

,

Então o limite 

Existe e é finito. 

Mostre que uma sequência crescente de reais positivos é sequência limite absoluto se, e só se, o limite

Existe e é finito. 

4 - (Putnam) Seja f : R -> R função contínua tal que 

Prove que f = 0 em [-1,1]. 

5 - (Putnam) Encontre c, L tais que 

~ Dicas e Soluções Parciais ~

1 - Use que, se P tem coeficientes inteiros e a,b são inteiros distintos, então 

Utilize tal propriedade repetidas vezes. 

2 - Considere uma face de P, veja qual a área máxima que a interseção de uma bola com uma tal face pode ser, e então use uma desigualdade entre as médias de ordem 2 e 3 para concluir. 

3 - Use uma desigualdade de Hölder na integral do denominador, com expoente . Note que, se 

Para terminar, mostre que a propriedade desejada é equivalente a  

Existir e ser finito 

4 - Mostre que f (0) = 0, escreva 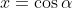, e itere o processo. Você pode precisar provar que vale primeiro para x da forma 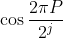, e usar um argumento de densidade. 

5 - Calcule a integral de cima por partes. c = - 1 deve funcionar. Para achar L apropriado, separe a integral entre 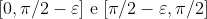, e faça algumas estimativas. Talvez mudar coordenadas seja interessante.