Este é outro post sobre a aplicação da derivada, agora relacionado a outro tipo de derivada: a derivada segunda. Mas, antes, veremos derivadas de ordens maiores do que 1.
As derivadas de ordens maiores que um são as tais que:
A -ésima derivada de uma função pode ser posta da seguinte maneira:
Sendo (n-1)-ésima derivada da função.
Comecemos pela derivada segunda. Esta é, das que tem ordem maior do que um, a de mais importância para nós.
Vejamos a seguinte função: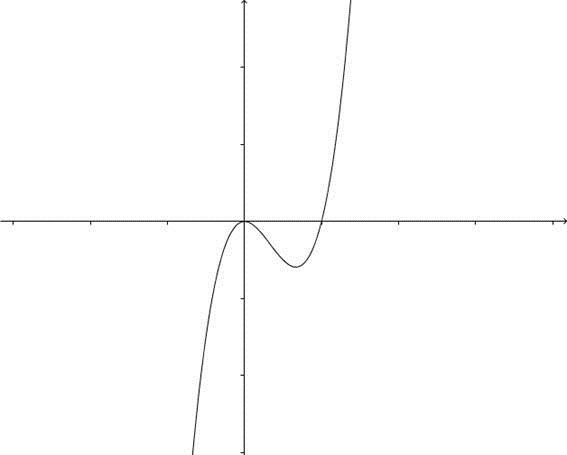
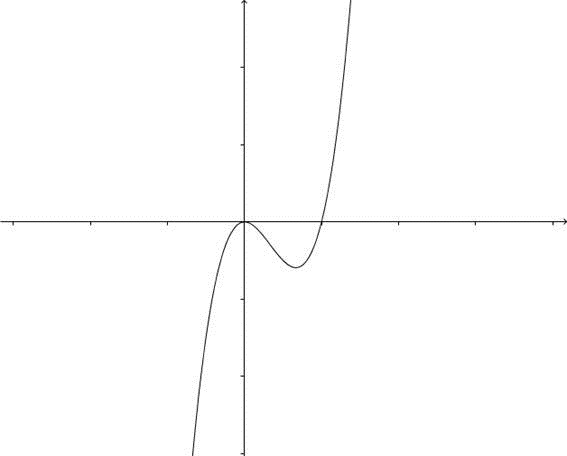
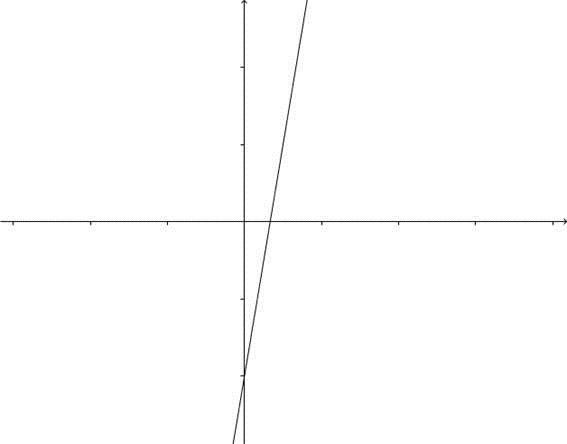
. Reparem que, como vimos, podemos achar dois pontos de máximo ou mínimo: um de máximo e outro de mínimo. Mas, e se quisermos achar o exato ponto em que podemos saber que a concavidade mudará? Reparem nas figuras abaixo:
Reparem que o ponto mínimo da derivada é o mesmo em que a derivada segunda se iguala a zero. Até aí, são resultados que poderíamos prever. Mas há outro fato: esse mesmo ponto coincide com um ponto na primeira função, e este ponto, se repararmos bem, é o ponto aonde a concavidade (“barriga” da curva) voltada para cima se encontra com a concavidade voltada para baixo. A esse ponto, nós chamamos de ponto de inflexão da função, ou ponto aonde a concavidade da curva muda. Em matemática,
Exemplo: Na mesma função do exemplo, calcule o ponto de inflexão e a equação da tangente naquele ponto.
Solução: Derivando a primeira vez, obtemos
E a segunda derivada é
Para calcular , substituímos
na função, tendo:
Ou seja, o ponto de inflexão é . Agora vamos calcular a tangente naquele ponto. Temos que o coeficiente angular da tangente naquele ponto é
substituído na derivada primeira, que é
Então, sua equação é
Para acharmos C, é só notar que , ou seja:
Ficando com a equação da tangente
Agora, vamos passar a outra utilidade da derivada segunda, que tem muito a ver com a que acabamos de relatar: achar o sentido da concavidade de uma curva qualquer. Reparem, naquelas imagens das três funções, que, quando a derivada segunda é negativa, a função tem concavidade voltada para baixo, e quando a derivada segunda é positiva, a curva tem concavidade voltada para cima. Generalizando, obtemos:
Podemos usar esse resultado para descobrir se o ponto em que a derivada primeira se anula é máximo ou mínimo: fica óbvio que, quando a concavidade é para baixo, há um ponto máximo, e quando a concavidade é para cima, há um ponto mínimo.
Exemplo: Na mesma função, calcule os pontos em que a derivada se iguala a zero e diga qual deles é máximo e mínimo, sem consultar o gráfico.
Solução: Primeiro, derivando:
Para descobrir qual é um máximo local e qual é um mínimo local, derivamos de novo, produzindo
Substituindo os dois valores de , obtemos
Tendo que no ponto em que a função assume um máximo, pois a derivada segunda é negativa, então a concavidade é voltada para baixo, e no ponto em que
a função assume um mínimo, pois a derivada segunda é positiva, então a concavidade da curva é voltada para cima.

Comentários
Postar um comentário
Você pode comentar! A equipe do blog encoraja todos a comentar.
Porém, lembre-se que comentários que desrespeitem as regras abaixo serão excluídos:
-É proibido ofender qualquer pessoa ou grupo em seu comentário.
-Os comentários deverão ser minimamente relacionados com o tópico. Lembrem-se, estamos falando de um blog de matemática!
-Proibido flood.
-Proibido palavras de baixo calão.
-Proibido colocar qualquer tipo de conteúdo improprio para menores de 18 anos (há menores de idade que acessam o blog).
A equipe do blog agradece seu comentário, e tenha certeza que será muito enriquecedor. Tentaremos respondê-los o quanto antes possível.