Esse é o primeiro de uma série em 4 partes sobre a unidade imaginária e os números complexos. Serão organizados da seguinte maneira:
1. Introdução e Breve História
2. Trigonometria e Números Complexos; Outras formas de representar o Complexo
3. Polinômios e os Números Complexos
4. Post Extra e outras relações dos Números Complexos
O conjunto dos números complexos é aquele que abrange o conjunto dos Reais (todos os números que definitivamente existem, aqueles que existem “concretamente”) e também abrange os números compostos pela unidade imaginária. A unidade imaginária é definida como o número que tem a propriedade de ser

Sendo i a unidade imaginária. Todo número complexo pode ser expresso da seguinte forma:
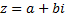
Sendo a e b números reais.
História
O estudante do ensino médio que aprende sobre números complexos geralmente o aprende para resolver equações do segundo grau com determinante negativo.
Entretanto, o estudo dos números complexos vem do estudo das equações do terceiro grau, ou cúbicas. Antes do grande “descobridor” dos complexos, Bombelli, todos os discriminantes de equações de segundo grau e de outros graus, quando negativos, eram apenas desconsiderados, e o problema ao qual a equação estava atrelada era considerado sem solução.
O primeiro indício de um “surgimento” dos complexos viria com Cardano (um post, ainda nessa semana, falará sobre demonstrações da resolução de equações de graus de 1 a 4), ao resolver uma equação do segundo grau, em sua famosa obra Ars Magna. Num problema ele pretendia achar o ponto dentro de um segmento que vale dez e o produto dos dois segmentos formados forme 40. Ele chama, então, os segmentos formados pelo ponto de x e 10-x. Então, formando uma equação, ele tem

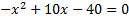
As Soluções dessa equação são . Cardano, se preparando para considerar seu problema sem solução, já que a raiz é de um número negativo, reparou que
. Cardano, se preparando para considerar seu problema sem solução, já que a raiz é de um número negativo, reparou que

Que era a solução que ele desejava. Ele, então, chamou esses resultados obtidos de soluções sofísticas da equação, já que elas eram, como o próprio disse, tão sutis quanto inúteis.
Mas o real idealizador dos números complexos, se podemos dizer, é o italiano seguidor de Cardano, Raphael Bombelli. Bombelli, como admirador de Cardano, leu totalmente sua publicação. Mas, descontente com alguns detalhes, ele resolveu publicar seu próprio (e influente) estudo: l’Algebra. Nesse estudo, Bombelli se depara com uma equação cúbica,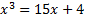 , cuja solução seria
, cuja solução seria

Mas, como vemos, a raiz quadrada dentro da cúbica é negativa, fazendo o número não “existir”. Mas, logo após, ele percebe que 4 também é uma solução da equação cúbica proposta. Então, Bombelli tem uma ideia para aquele problema: ele considera que, mesmo que imaginariamente, haja um número da forma que seja a raiz cúbica de
que seja a raiz cúbica de  , e também um número
, e também um número 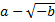 , que seja raiz cúbica de
, que seja raiz cúbica de 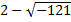 . Com esses números, ele pensa que esses satisfaçam a
. Com esses números, ele pensa que esses satisfaçam a

E, para sua felicidade, ele acha a=2. Daí, ele deduz que b=1, ao voltar à equação principal. Então ele tem que

E ele finalmente conclui que seu achado é revolucionário. Como ele diz em sua obra, ele tinha em mente que a “tal” imaginária sempre “existisse” (é meio paradoxal mesmo). Daí, ele já parte para as regras de multiplicação da unidade imaginária em sua obra. Para se ter uma ideia, o pensamento de Bombelli da unidade imaginária só seria formalizado quase 60 anos depois, quando Girard introduziu o símbolo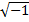 . Já o popular símbolo i só seria introduzido 105 anos depois de l’Algebra, por Leonhard Euler.
. Já o popular símbolo i só seria introduzido 105 anos depois de l’Algebra, por Leonhard Euler.
Vou parar por aqui, pois esta história é muito mais extensa e rica. Para maiores detalhes, leia o artigo que inspirou essa breve história:
A emergência dos números complexos,
César Polcino Milies, RPM 24

Forma Geral:
Todo número complexo pode ser escrito como
![clip_image004[1] clip_image004[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiG3IVbYI7lY8UEZWd1kGX03VIkQrkxieuwGtiUBZBFVB6hBjB0-0mgB8XLhU3vCixwdIE6UfLE6LMvo4ZRWY0qnynt9WbgkKHnyf7_EyW_w26gqoDOYPCU4GhlSWWEnQ8v0vVJ7r6e-Y8/?imgmax=800)
Com i a unidade imaginária.
Módulo:
O módulo de um número complexo é

Operações Essenciais Com Números Complexos:
Adição:

Subtração:

Multiplicação:

Divisão:

Agora, vamos introduzir o conceito de CONJUGADO do número complexo. Veja:
O conjugado de um complexo
![clip_image004[2] clip_image004[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhj5eyi4Rte_Fw-g52JxaQmWVpOb2XHyH20rOWDN-oarm9u2jUYdOZWROvAs-bZaEYmKF9mH14Zg8NBzMCNCf85KhP97AdLcvvJUBcxsrS7rluE_pOWvNpmxm63Re9tJQfcG1Iuz8O1P-E/?imgmax=800)
É

Podemos prosseguir, multiplicando o numerador e o denominador pelo conjugado do complexo no denominador, obtendo
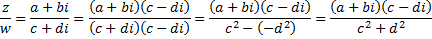

Agora, algumas propriedades do conjugado:

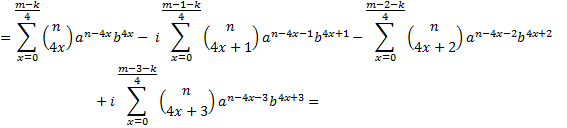

Logo vemos que esse é um conjugado. O conjugado desse conjugado é


Fazendo , temos
, temos


Isso mostra que a potência do conjugado é igual ao conjugado da potência.
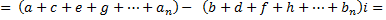



Que se verifica.
Para n+1, temos
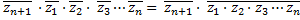
Sendo e
e  , temos
, temos


Mas como e
e  , temos
, temos



Que demonstra a fórmula para n+1, verificando a validade da fórmula.
Bom, gente, é só. Espero que vocês achem útil o post. Se você gostou do blog, inscreva por e-mail e no blog para receber as novas atualizações e curta nossa página no Facebook. Todas essas opções se encontram na barra lateral do blog e abaixo da postagem. Para melhorar a qualidade de nossas postagens avalie o conteúdo aqui embaixo. É rapidinho! Lembre-se que todo tipo de comentário que respeitar as regras é bem vindo.
Até Mais,
João Pedro.
1. Introdução e Breve História
2. Trigonometria e Números Complexos; Outras formas de representar o Complexo
3. Polinômios e os Números Complexos
4. Post Extra e outras relações dos Números Complexos
O conjunto dos números complexos é aquele que abrange o conjunto dos Reais (todos os números que definitivamente existem, aqueles que existem “concretamente”) e também abrange os números compostos pela unidade imaginária. A unidade imaginária é definida como o número que tem a propriedade de ser
Sendo i a unidade imaginária. Todo número complexo pode ser expresso da seguinte forma:
Sendo a e b números reais.
História
O estudante do ensino médio que aprende sobre números complexos geralmente o aprende para resolver equações do segundo grau com determinante negativo.
Entretanto, o estudo dos números complexos vem do estudo das equações do terceiro grau, ou cúbicas. Antes do grande “descobridor” dos complexos, Bombelli, todos os discriminantes de equações de segundo grau e de outros graus, quando negativos, eram apenas desconsiderados, e o problema ao qual a equação estava atrelada era considerado sem solução.
O primeiro indício de um “surgimento” dos complexos viria com Cardano (um post, ainda nessa semana, falará sobre demonstrações da resolução de equações de graus de 1 a 4), ao resolver uma equação do segundo grau, em sua famosa obra Ars Magna. Num problema ele pretendia achar o ponto dentro de um segmento que vale dez e o produto dos dois segmentos formados forme 40. Ele chama, então, os segmentos formados pelo ponto de x e 10-x. Então, formando uma equação, ele tem
As Soluções dessa equação são
Que era a solução que ele desejava. Ele, então, chamou esses resultados obtidos de soluções sofísticas da equação, já que elas eram, como o próprio disse, tão sutis quanto inúteis.
Mas o real idealizador dos números complexos, se podemos dizer, é o italiano seguidor de Cardano, Raphael Bombelli. Bombelli, como admirador de Cardano, leu totalmente sua publicação. Mas, descontente com alguns detalhes, ele resolveu publicar seu próprio (e influente) estudo: l’Algebra. Nesse estudo, Bombelli se depara com uma equação cúbica,
Mas, como vemos, a raiz quadrada dentro da cúbica é negativa, fazendo o número não “existir”. Mas, logo após, ele percebe que 4 também é uma solução da equação cúbica proposta. Então, Bombelli tem uma ideia para aquele problema: ele considera que, mesmo que imaginariamente, haja um número da forma
E, para sua felicidade, ele acha a=2. Daí, ele deduz que b=1, ao voltar à equação principal. Então ele tem que
E ele finalmente conclui que seu achado é revolucionário. Como ele diz em sua obra, ele tinha em mente que a “tal” imaginária sempre “existisse” (é meio paradoxal mesmo). Daí, ele já parte para as regras de multiplicação da unidade imaginária em sua obra. Para se ter uma ideia, o pensamento de Bombelli da unidade imaginária só seria formalizado quase 60 anos depois, quando Girard introduziu o símbolo
Vou parar por aqui, pois esta história é muito mais extensa e rica. Para maiores detalhes, leia o artigo que inspirou essa breve história:
A emergência dos números complexos,
César Polcino Milies, RPM 24
Forma Geral:
Todo número complexo pode ser escrito como
Com i a unidade imaginária.
Módulo:
O módulo de um número complexo é
Operações Essenciais Com Números Complexos:
Adição:
Subtração:
Multiplicação:
Divisão:
Agora, vamos introduzir o conceito de CONJUGADO do número complexo. Veja:
O conjugado de um complexo
É
Podemos prosseguir, multiplicando o numerador e o denominador pelo conjugado do complexo no denominador, obtendo
Agora, algumas propriedades do conjugado:
- .
Prova: A demonstração vem com

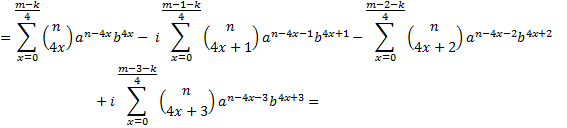

Logo vemos que esse é um conjugado. O conjugado desse conjugado é


Fazendo


Isso mostra que a potência do conjugado é igual ao conjugado da potência.
· Prova: Por indução, para n=1, temos
Que se verifica.
Para n+1, temos
Sendo
Mas como
Que demonstra a fórmula para n+1, verificando a validade da fórmula.
Bom, gente, é só. Espero que vocês achem útil o post. Se você gostou do blog, inscreva por e-mail e no blog para receber as novas atualizações e curta nossa página no Facebook. Todas essas opções se encontram na barra lateral do blog e abaixo da postagem. Para melhorar a qualidade de nossas postagens avalie o conteúdo aqui embaixo. É rapidinho! Lembre-se que todo tipo de comentário que respeitar as regras é bem vindo.
Até Mais,
João Pedro.
Olá João,
ResponderExcluir"... abrange o conjunto dos Reais (todos os números que definitivamente existem, aqueles que existem “concretamente”) e também abrange os números compostos pela unidade imaginária."
Não vejo como distinguir as "existências" dos números reais e dos complexos... O que você quer dizer com essa frase?
Olá Renato,
ExcluirAcho que ele quis dizer que, embora os complexos existam você não pode dizer por exemplo: "hoje, comprei a+bi pães" no máximo "a pães".
Isso é minha opnião, só vendo com ele.
Olá, Renato. "... abrange o conjunto dos Reais (todos os números que definitivamente existem, aqueles que existem “concretamente”) e também abrange os números compostos pela unidade imaginária."
ResponderExcluirEsta foi apenas uma citação para os que entendem "menos" do assunto possam pegar a ideia do conjunto dos números complexos. Diria que os Reais têm uma existência no mundo à nossa volta: são utilizados para medir, são medidas que há na natureza.
Os complexos, ao contrário, não podem ser utilizados para medir nada, pois não podemos ordenar os complexos por tamanho, já que diferentes complexos podem ter o mesmo módulo (o que vai os diferenciar nesse caso é seu argumento).
Espero que tenha esclarecido,
Atenciosamente, João Pedro.