Trazemos hoje uma miscelânea de assuntos sobre geometria com contas. Vamos falar sobre alguns dos principais tópicos neste post, e mais tópicos interessantes no próximo post. Começamos por algumas definições que já devem ser inerentes à maioria dos que visitam o blog hoje, mas, a quem não está lembrado ou não conhece muito bem, vale a pena lembrar. Evoluímos gradativamente o nível de dificuldade dos assuntos, até terminar com um teorema bem conhecido e utilíssimo sobre cevianas (O próximo teorema sobre cevianas, o de Ceva, será abordado nos próximos posts da série).
Definição 1: Dizemos por seno (sen) a razão entre o cateto oposto a um ângulo e a hipotenusa do triângulo retângulo que contém este ângulo. O cosseno (cos) é a razão entre o cateto adjacente e a mesma hipotenusa, e a tangente (tg) é a razão entre o cateto oposto e o adjacente (também pode ser vista como a razão entre o seno e o cosseno).
Definição 2: Definimos as funções cossecante, secante e cotangente (cossec, sec e cotg, respectivamente) como
Teorema fundamental da trigonometria: para qualquer x real,
Alternativamente,
Demonstração: Em qualquer triângulo retângulo, seus lados podem ser escritos como
Logo, aplicando Pitágoras,
Dividindo esta relação por cos² x e sen ² x, obtemos, respectivamente, a primeira e a segunda relações.
Fórmula de adição e subtração de arcos:
Fórmulas do arco duplo:
Fórmulas do arco metade:
Demonstração: Seja z=cis a e w=cis b. Então, pela multiplicação de complexos, zw = cis (a+b). Mas, utilizando a multiplicação no sentido manual,
Pela identidade das partes reais e imaginárias, devemos ter
Além disso, para definir a tangente de (a+b), temos de fazer a razão entre seno e cosseno:
Dividindo o numerador e o denominador por cosacosb,
Para obter as fórmulas (a – b), só temos que saber que cos (-b) = cos b , sem (-b) = - sen b e tg (-b) = - tg b e efetuar as transformações necessárias. Para obter as fórmulas do arco duplo, efetuar a=b basta (em particular, nas duas últimas fórmulas para o cosseno do arco duplo, apenas efetue que sen² a = 1 – cos²a). Para efetuar as fórmulas do arco metade, utilizamos a fórmula do cosseno do arco duplo (com ajuda de radicais), e a tangente do arco duplo é facilmente obtenível a partir da razão entre seno e cosseno. ■
Transformação da soma em produto (Fórmulas de Prostaférese):
Demonstração: As duas primeiras são obtidas somando fórmulas das somas e diferenças dos arcos, chamando a=x+y, b=x – y e achando que x= (a+b)/2, y =(a – b)/2. A terceira é só uma aplicação de que sen (90 – a) = cos a, e as 3 ultimas são apenas somas (e diferenças, não importa) de fórmulas de adição e/ou subtração de arcos. ■
Lei dos Senos: Em um triângulo ABC de lados a,b,c e ângulos respectivos α,β,γ, e de circunferência circunscrita de raio R, então
Lei dos Cossenos: Em um triângulo ABC, onde o ângulo , o lado oposto a α é a e os outros lados são b,c, então temos que
Lei das Tangentes: Em um triângulo ABC de lados a,b,c e ângulos respectivos α,β,γ, vale que
E vale o análogo pros outros lados/ângulos.
Demonstração da LdT: Da lei dos senos,
Utilizando Prostaférese,
■
Transformação Útil para resolver problemas: Quando as medidas do triângulo não forem especificadas, apenas utilize que R=1/2. Isso fará com que os lados sejam equivalentes aos senos de seus ângulos.
Proposições baseadas na transformação:
O triângulo tem perímetro
Tem área
E o raio da circunferência inscrita é igual a
Demonstração: Temos que
A segunda proposição vem de que, em um triângulo qualquer de lados a,b e ângulo entre os lados α tem área
E daí sai diretamente.
Para a ultima proposição, precisaremos do seguinte lema:
Lema:
Onde p é o semiperímetro do triângulo e r, o inraio
Demonstração: Só temos de particionar o triângulo em três menores, cujas alturas são r (isso é fácil de fazer, apenas ligue o incentro a cada um dos vértices). Assim, ao calcular a área teremos
■
Assim,
Que termina as proposições. ■
Teorema de Stewart: Seja um triângulo, como na figura:
Então devemos ter
Demonstração: Se o ângulo entre d e m for, chamemos, θ, utilizando lei dos cossenos no triângulo de lados d,m e c:
Fazendo o mesmo no triângulo ao lado,
Vamos fazer uma combinação linear da primeira e a segunda equação:
Somando,
Como queríamos. ■
Teorema de Stewart Aplicado às Medianas: Em um triângulo, a medida de sua mediana relativa ao lado a é
Demonstração: É evidente ao chamarmos n=m=a/2. ■
Observação: Não demonstramos, por abreviação, a lei dos senos ou cossenos. Deixamos isto como uma tarefa não muito difícil ao leitor curioso. Tente!
Espero que tenham gostado do post. Fiquem ligados no blog sobre mais artigos úteis de matemática.
Avalie o post aqui embaixo! É rapidinho, demora no máximo três segundos.
Lembre-se: todos podem comentar e deixar sua opinião ou crítica no post, desde que esta seja bem-educada.
Fontes:
SHINE, C.Y. – Geometria com contas (como acessado em http://cyshine.webs.com/Geoconta.pdf)
CARMO, M.P. do, MORGADO, A.C., WAGNER, E. Trigonometria e Números Complexos. SBM, Brasil, 1992.






![clip_image070[1] clip_image070[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgfBp0iKsEiX-7hT7FzloH8pdKjKqkRFtRvkZrAOwne6bNrVCJVjzXZqJkjVHCvQHyJYErgBMy0ccEnWey5KdyPQIMW46nzvUV0L4jZ-5kN7To2u45Z01vO34oHrgj0cD0qqPIYHQ5RMQI/?imgmax=800)
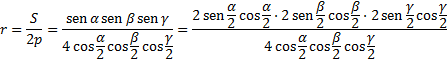


Comentários
Postar um comentário
Você pode comentar! A equipe do blog encoraja todos a comentar.
Porém, lembre-se que comentários que desrespeitem as regras abaixo serão excluídos:
-É proibido ofender qualquer pessoa ou grupo em seu comentário.
-Os comentários deverão ser minimamente relacionados com o tópico. Lembrem-se, estamos falando de um blog de matemática!
-Proibido flood.
-Proibido palavras de baixo calão.
-Proibido colocar qualquer tipo de conteúdo improprio para menores de 18 anos (há menores de idade que acessam o blog).
A equipe do blog agradece seu comentário, e tenha certeza que será muito enriquecedor. Tentaremos respondê-los o quanto antes possível.