Hoje falaremos de desigualdades, enunciando e demonstrando as mais úteis e conhecidas, mas não deixaremos de lado as desigualdades pouco conhecidas; muitas desigualdades pouco faladas matam mais problema que a mais famosa de todas. Porém, quando falamos de desigualdade, temos que ter em meta principalmente o que se quer provar. Quando se conhece um número grande de desigualdades, fica fácil provar qualquer desigualdade, desde que você tenha um olhar esperto.
As desigualdades se dividem em dois principais ramos: desigualdades mais sintéticas, e as desigualdades mais brutais, por assim dizer. Vamos explicar de que tipo é cada, mas com certeza todas são úteis na hora de resolver os problemas. Todos os problemas daqui serão de algum tipo de olimpíada, como vocês verão. Alguns mais imediatos que outros, mas todos são fazíveis.
Portanto, comecemos com algumas desigualdades óbvias:
Desigualdade Fundamental: Para todo x real, vale que
Ora, é um tanto quanto óbvia essa desigualdade, mas é mais que útil! Muitos problemas morrem sem utilizar nada além disso, problemas inclusive da IMO! Porém, outros necessitam de teoremas mais sofisticados.
Vamos ver alguns deles agora:
A demonstração para esta desigualdade pode ser vista clicando aqui. Para o post não ficar grande demais, não a repetiremos.
Esta é a desigualdade mestra pra todo mundo que começa a estudar desigualdades. Com ela, você consegue fazer mil e uma coisas. Darei exemplo bastante interessante, que, a primeira vista, parece complicado, mas ao utilizar esta desigualdade tudo se torna simples:
Exemplo 1: (USAMO) Sejam a,b,c reais positivos. Prove que
Demonstração: Sabemos que
Utilizando a desigualdade entre as médias em a² + b², esta expressão se torna
Logo,
Que nos dá
Como não há nada de especial com a,b, podendo combinar c também com cada um dos dois da dupla, obtemos desigualdades análogas para os outros termos da soma. Ao final, obtém-se o resultado desejado. ■
Este exemplo mostra a utilidade desta poderosa ferramenta. Ela também nos dá o importantíssimo
Demonstração: Por MA-MG, temos que
Multiplicando as duas desigualdades, obtemos o desejado. ■
Pode não parecer, mas este Corolário é utilíssimo. Quando estivermos falando de Chebyshev seu poder será evidenciado. Depois daremos exemplos. Agora, vamos prosseguir:
Demonstração: Seja
Este polinômio é uma soma de quadrados, portanto, ele é maior ou igual que zero. Logo, ao analisar o determinante, este deve ser menor ou igual a zero. Mas isso significa
De onde segue a desigualdade. Reparem que para obter igualdade, temos que ter cada quadrado igual a zero, isto é,
E isto termina a prova. ■
Agora, vamos a um exemplo da utilidade desta desigualdade:
Solução: Multiplicando as duas igualdades,
Mas, por Cauchy-Shwarz,
Com igualdade só ocorrendo se
Ou seja,
E a solução segue. ■
Exemplo 3: (IMO-1995) Sejam abc = 1 três reais positivos. Prove que
Demonstração: Resolveremos este problema de outra maneira depois. Porém, agora vamos efetuar uma substituição interessante. Seja a = 1/x, b = 1/y e c = 1/z. Logo, o produto dos três continua sendo 1, e a desigualdade se torna
Mas, por Cauchy-Shwarz,
Mas
De onde segue a desigualdade proposta. ■
Essas desigualdades até agora mostradas são bem óbvias, porém as próximas não são tão óbvias. Contudo, são as que mais ajudam na hora do aperto. Enunciaremo-nas, então:
Então vale que
Com igualdade se, e somente se, os a’s ou os b’s forem iguais.
Demonstração: Queremos mostrar, na verdade, que
Mas (verifique), o lado esquerdo é igual a
Que é verdadeiro, pois, se i < j, então bi < bj e ai < aj,, e vice e versa. Logo, o produto é sempre positivo, fazendo com que as somas sejam sempre positivas. Reparem que a condição de igualdade é obviamente verificada. ■
Essa, ao meu ver, é uma desigualdade essencial no arsenal de quem quer resolver problemas de desigualdade. Muitos problemas morrem facilmente utilizando-a. Por isso, vamos dar exemplos:
Demonstração: Podemos supor que os a’s estejam bem ordenados. Logo, temos que
Assim, usaremos Chebyshev nesta sequência. Logo,
Agora que vem o nosso Corolário! Por ele, temos que
A desigualdade do enunciado segue da multiplicação destas duas últimas. ■
Exemplo 5: Sejam a,b,c reais positivos dados e n natural. Então, prove que
Então, utilizaremos Chebyshev, que nos dá
Por sua vez, do nosso Corolário,
Multiplicando,
Que é o resultado que queremos. ■
Acho que já ficou bem evidente a utilidade da desigualdade de Chebyshev aliada ao nosso corolário. Agora, algo que talvez não tenha ficado muito óbvio é a consequência da desigualdade de Chebyshev, expressada no seguinte
Demonstração: A cargo do leitor. Porém é apenas utilização direta de indução e da desigualdade de Chebyshev. ■
Temos, ainda, uma desigualdade ligada à de Chebyshev: a desigualdade das permutações.
Desigualdade das Permutações: Sejam a1 ≤ a2 ≤ a3 ≤ ... ≤ an e b1 ≤ b2 ≤ b3 ≤ ... ≤ bn duas sequências de reais positivos. Então, se ai1, ai2,..., ain e bi1, bi2,..., bin são duas permutações, respectivamente, das sequências, então
Demonstração: Deixada a cargo do leitor. (Dica: Tente fatorar as expressões, e provar que elas são, definitivamente, maiores ou menores que zero).

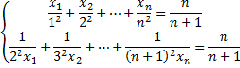






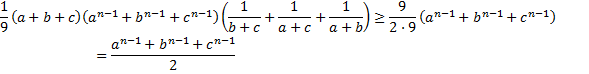
a continuação desse artigo já esta disponível?
ResponderExcluirBelo artigo :D