Fórmulas Trigonométricas Através de Números Complexos

Um amigo meu, recentemente, teimou que “minha demonstração para o cosseno e o seno das somas está incorreta”. Ele se refere à demonstração contida aqui, mesmo ela estando muito abreviada. Tentei, algumas vezes, lhe explicar verbalmente como era e no que se baseava a demonstração, mas julgo que, mesmo por falha minha, não devo ter me expressado direito, fazendo com que ele mantenha, até hoje, a insistência em que minha demonstração está incorreta.

Pois bem, caro amigo! Esta demonstração mais do que completa vai especialmente para você. Vou detalhá-la desde o início, e mostrar que, realmente, é uma demonstração muito mais prática sobre o cosseno e o seno da soma de arcos, muito mais natural que a usual demonstração.

Repare também que não faz uso da tal fórmula de Euler (), que implicaria um suposto uso da fórmula de expansão de Taylor, que, por sua vez, implicaria na utilização da derivada do seno, que contém o nosso teorema a ser demonstrado. Não tem nada a ver com isso. É uma prova totalmente elementar, só utilizamo-nos da multiplicação de números complexos e de um pouco de pensamento vetorial.

Pois bem, cortando-se o papo, vamos à ação. A prova será feita por etapas, começando pelo

Lema 1: Seja Então, ao multiplicar este número complexo por i, obtemos . Em outras palavras, equivale a rotacionar o vetor em 90 graus.

Demonstração: Repare que

Porém, por trigonometria básica, , e .

Logo,

Como queríamos demonstrar.

Fato 1: Ao multiplicar um complexo por uma constante, este não muda seu argumento. De fato, equivale a multiplicar um vetor por um escalar, que, como sabemos, nunca muda sua direção.

Lema 2: Ao multiplicar dois complexos distintos, digamos e , então, ao colocá-los em sua forma vetorial (ou trigonométrica), equivale-se a rotacionar um dos vetores e multiplicar seus módulos.

Demonstração: Seja

Logo, multiplicando,

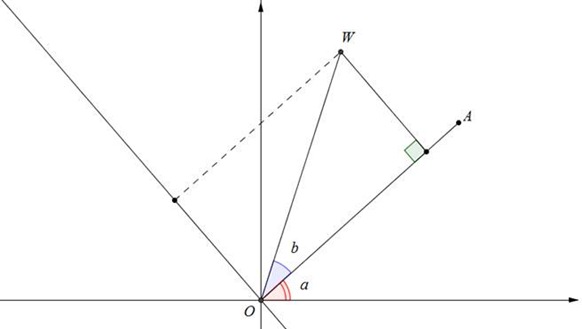
Logo, o resultado da multiplicação dos dois complexos é o complexo correspondente à diagonal do paralelogramo de lados e . Em linguagem vetorial, equivale à soma vetorial entre os dois vetores e .

Como, pelo nosso primeiro lema, os dois vetores anteriormente descritos são ortogonais, é fácil ver que o ângulo que o vetor resultante fará com o vetor é de . Portanto, concluímos o desejado, ou seja, o argumento do vetor resultante da multiplicação é a soma dos argumentos.

Agora, nosso teorema fica fácil de demonstrar:

Teorema do Cosseno e do Seno da Soma de arcos: Sendo reais*, então é sempre válido que

Demonstração: Nada mais é do que uma bijeção: vamos contar de duas maneiras o valor da parte real e da imaginária do produto de números complexos , onde

Pela multiplicação usual, ou seja, utilizando as regras convencionais de multiplicação, obtemos

Porém, pelo nosso lema anterior,

E os resultados seguem por igualdade entre partes reais/imaginárias.

Para mais resultados interessantes, práticos e, em muitos casos, improváveis, acessem o blog! Teremos muitas novidades por vir.

Fonte:

[1] P. DO CARMO, Manfredo; C.MORGADO, Augusto; WAGNER, Eduardo. Trigonometria e Números Complexos. 3ª edição. Rio de Janeiro, RJ, SBM, 2005.