Hoje achei este arquivo perdido em meu computador. Se trata de um projeto antigo sobre escrever sobre fórmulas para resolução de equações de grau menor ou igual a 5, de quase dois anos atrás. Assim, vamos analisar todos os principais casos de equações, até os realmente triviais. Não deixaremos exercícios, pois isto é apenas um post para os curiosos que desejam saber uma fórmula para a equação de terceiro/quarto grau. Comecemos pela
Demonstração 1: Demonstração da fórmula de resolução da equação do primeiro grau
Esse é o caso mais fácil de se deduzir: temos
Embora tenha sido um exemplo um tanto quanto rápido, a dificuldade tende a aumentar junto com o grau da equação. Portanto, continuemos:
Demonstração 2: Demonstração da fórmula de resolução da equação do segundo grau
Temos a seguinte equação do segundo grau:
Efetuando , com o produto notável, temos
Efetuando a substituição em z, temos
Refazendo , recuperamos a fórmula
Que é a famosa fórmula quadrática (também chamada, erroneamente, de fórmula de Bháskara. Bháskara, na verdade, contribuiu para a matemática sim, mas as equações do segundo grau já eram bem conhecidas em sua época). ■
Agora começarão os métodos não convencionais e criativos para obter as fórmulas. Sugerimos ao leitor que realmente está interessado que preste muita atenção, alguns detalhes se mostram muito técnicos.
Demonstração 3: Demonstração da fórmula de resolução da equação do terceiro grau
Tomemos a seguinte equação do terceiro grau:
Efetuando a substituição , com o produto notável, temos
Com e com
, resultamos em uma equação da forma
Agora, se pudermos colocar , para quaisquer valores de u e v, então temos
Agora, vamos buscar uma maneira de zerar, em função de u + v, a equação. Uma maneira é fazer
Mas, como (u+v) = x , temos
Daí tiramos que
Como o sistema é simétrico em A,B, então podemos arbitrá-las:
Que é a fórmula de Cardano-Tartaglia. É claro que existe uma forma de fazer esta equação ainda mais relacionada com a original, porém é resultado de modificações algébricas muito entediantes e cansativas. Além do mais, o cálculo de p e q não é difícil: é só substituir os valores originais na equação. ■
Demonstração 4: Demonstração da fórmula de resolução da equação quártica
Tomemos a seguinte equação quártica:
Dividindo por (como sempre, para gerar uma equação mônica), temos
Fazendo , obteremos (as contas são suficientemente exaustivas para omiti-las daqui, porém recomendamos que o leitor as faça para treinar) um polinômio da forma
Agora, pretendemos obter uma equação da forma
Que ficará fácil de resolver pela fórmula quadrática. Primeiro, tem alguns passos a seguir:
Como queremos que o segundo membro seja um quadrado perfeito, vamos adicionar um número qualquer k a ambos os lados, de modo que o membro da esquerda continue um quadrado perfeito, e o da direita vire um quadrado perfeito. Temos, então
Agora, para o membro da direita ser um quadrado perfeito, então o Delta (discriminante da equação do segundo grau do membro à direita, quando analisamos na fórmula quadrática) tem de ser zero. Esse discriminante é
Então, para achar o número que satisfaça o requisito do membro à direita ser um quadrado perfeito, devemos resolver a equação acima. Pela fórmula de Cardano-Tartaglia para cúbicas, temos (pelo menos) uma solução real para tal equação de terceiro grau em k. Podemos também utilizarmo-nos do truque da demonstração anterior para reduzir ao nosso caso estudado, e daí achamos k. Temos, com
A equação
Que é o desejado. Reparem agora que não demos uma fórmula explícita para z: é quase impossível fazer tanta conta! Reparem que daríamos k em sua forma de resolução de cúbica, o que ainda demandaria modificações e, além disso, este apareceria em um radical. Logo após, apareceria este radical dentro de mais um radical, o que é suficientemente cansativo para não fazermos, porém o leitor que anseia por respostas teve suas perguntas quase totalmente respondidas. ■
Referências Bibliográficas:
- Inspirado em artigos avulsos lidos pela internet, porém as demonstrações foram todas desenvolvidas pelo autor.
Avalie o post aqui embaixo, é rápido! Alguma correção, dúvida, elogio, questão ou comentário, poste aqui. O seu comentário é muito bem vindo.



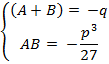




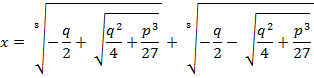

Oi, João Pedro!
ResponderExcluirParabéns pelo desenvolvimento do artigo. Bem organizado e lógica impecável.
Uma vez li em algum Almanaque Abril que as equações quínticas são resolúveis transcedentemente por funções elípticas mas, até agora não encontrei nem em livros e nem na net.
Outro assunto que também que é difícil encontrar na net são as fórmulas para sen(nx) e cos(nx).
Uma curiosidade. Só vejo vc postando. Antes era uma equipe, não?
Um abraço!
Oi, Aloísio!
ResponderExcluirObrigado pelos elogios, sempre é bom, principalmente de um companheiro de blogs!
Quanto a funções elípticas e resolução da equação quíntica, não sei de nada realmente interessante. Gostaria de saber da demonstração de Abel para a inexistência da solução por radicais, pois nunca a encontrei.
As fórmulas do sen(nx) e cos(nx) são relativamente fáceis de se demonstrar, usando números complexos. Tenho um livro da União Soviética que tem isso, é interessante.
Quanto aos postadores, sei que eu tenho postado mais, porém o Eduardo (dudu) postou recentemente sobre bijeções, e o nosso outro postador, o Rafael Filipe, que não se apresentou ainda, está usando o perfil do blog (A Matemática Pura).
Espero ter tirado a dúvida rs
Abraço!
Olá João Pedro, muito bom o post, bem dinâmico. Fiquei com esta dúvida. Não seria assim
ResponderExcluir(x^2 + q + k)^2 = (x^2 + q)^2 + 2k(q + x^2) + k^2
ao invés de
(x^2 + q + k)^2 = (x^2 + q)^2 + 2k(q + x) + k^2
Até mais.
Olá, Paulo! Obrigado pelo elogio, mais uma vez é muito bom :)
ResponderExcluirQuanto à dúvida, é assim mesmo, como na primeira expressão. Desculpa pelo engano, já corrigi todos os possíveis erros.
Abraço!
Oi, amigão! Muito legal seu blog! Tenho um canal de vídeos de Matemática no YouTube, onde tento ensinar os assuntos de forma divertida, além de apresentar algumas curiosidades matemáticas. Se quiser visitar e, caso goste, divulgar em seu blog (para ter mais conteúdo), fique à vontade! :)
ResponderExcluirMatemática Rio: http://www.youtube.com/matematicario
Opa, Rafael! Obrigado pelos elogios :)
ExcluirQuanto ao teu canal, eu curti a iniciativa, achei organizado e bem legal! Gostaria de propor uma parceria entre os nossos meios de comunicação: eu divulgo o teu canal, que é mais didático que o meu blog, pro leitor quer precisa aprender desesperadamente, ou tem dificuldades, e você divulga o meu blog pro leitor que quer saber mais.
O que acha?
Abraço!
quanto e 80-3(x+9)=16-4x
ResponderExcluirOlá carolaine,
Excluireste blog não é destinado a tirar dúvidas de exercícios específicos. Tente aplicar o que foi ensinado neste post.
Até mais,
Eduardo
Ola, João Pedro, eu sou matemático e quero parabenizar você por esse seu blog é de excelente qualidade. Continue assim.
ResponderExcluir