Um resumo de métodos de Integração

A Matemática, por si só, já é um dos tipos mais puros e lindos de arte que se pode encontrar na natureza. Tudo da matemática, quando bem entendido, é algo extremamente surpreendente - ora, quem poderia prever um teorema como a reciprocidade quadrática de Gauss? Gauss mesmo achava sua lei tão bonita que, além de a chamar de teorema áureo, reza a lenda que ele teria escrito 8 demonstrações distintas da mesma, sendo a primeira com 19 anos de idade.

Mas não estamos aqui para falar da lei da reciprocidade quadrática de Gauss. Hoje vamos falar de uma forma de arte que, em minha opinião, é uma das mais bonitas da matemática: os métodos de substituição em integrais.

Para o leitor já familiarizado com um pouco de cálculo, sabe a importância das substituições em integrais, principalmente em integrais de produtos. Portanto, aqui começamos com nosso primeiro método importante: o método de Integração por Partes.

Teorema 1: Sejam u, v duas funções diferenciáveis. Então

Demonstração: Pela regra da derivada do produto, temos que

Integrando em relação x ambos os membros,

O que completa nossa demonstração. ■

Ora, uma fórmula razoavelmente óbvia não deveria ser tão útil, certo? Errado! Vamos mostrar exemplos de funções que, ao utilizarmos o método de integração por partes, ficam evidentemente simples de se resolver, por vários motivos:

Exemplo 1: Calcule

Resolução: Vamos resolver pelo métodos de integração por partes: seja e^-x = dv e sen x = u. Logo,

Agora, vamos utilizar o mesmo método para a integral à direita: e^-x = dv e cos x = u. Portanto,

Chamando nossa primeira integral de I, então temos

Este foi um exemplo um tanto quanto explicativo: o método de integração por partes serve para transformar uma integral complicada em, geralmente, uma equação linear! É claro, não é a única serventia do método - tem a mais óbvia. Aproveitaremos o exemplo abaixo para introduzir, desde já, o nosso segundo método e exemplificar a utilização acima:

Exemplo 2: Calcular

Resolução: Seja arctan x = u, dv = dx. Portanto,

Pois (arctan x)’= 1/(x²+1). Logo, basta avaliar a integral à direita. Fazendo

Então

Substituindo, encontramos

Portanto,

Que é, definitivamente, o resultado que desejamos. ■

Já deu para reparar qual o nosso novo método: fazer uma substituição conveniente de funções! O leitor pode até pensar: “ah, mas isto é óbvio! Substituir funções é algo bem razoável”. Pode até ser, mas a substituição da qual estamos falando visa nos facilitar as contas. Vejamos mais um exemplo:

Exemplo 3: Calcule

Resolução: A ideia, neste caso, é de completar quadrados: Como

E

Então podemos fatorar o denominador em

Logo,

Nossa substituição, à primeira vista, não era tão óbvia: fazer u = 6x + 5. Isto, à primeira vista, pareceria absurdo, mas agora parece muito razoável. Após a substituição, du = 6 dx. Portanto,

Que é o valor desejado. ■

Para finalizar nossa postagem bem resumida de métodos criativos de integração, vejamos o método mais criativo, ao meu ver: substituição trigonométrica. Criativo não no sentido de mais mirabolante, porém no que pode significar que, em muitos casos, uma integral difícil e aparentemente estranha pode ficar resolvível com a substituição trigonométrica. Para ilustrar, vamos ver exemplos:

Exemplo 4: Calcule

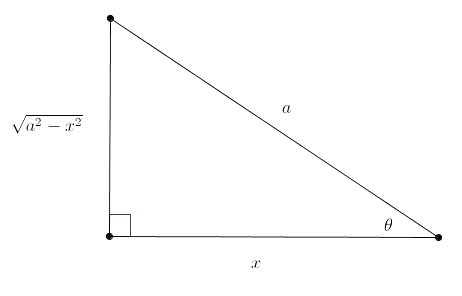
Resolução: Observe a figura abaixo:

Observe que x = a cos θ, e que . Logo, dx = a (- sen θ) dθ. Nossa integral se transforma em

Agora, vamos utilizar do método de integração por partes: seja sen θ dθ = dv, e tg θ =u. Logo,

Portanto, temos apenas de avaliar

Porém, é bem conhecido que

Logo,

Agora, vejamos um exemplo de um desafio, proposto na OBM-Universitária de 2010:

Exemplo 5: (OBM-U) Calcule

Resolução: Se tentarmos integrar normalmente, ou seja, tentar a integral para depois substituir de 0 a π/4, teremos um bocado de dor de cabeça. Portanto, vamos por partes. O trocadilho pode até ser ruim, mas a técnica, de fato, é poderosa: Modificando a integral,

Agora, integrando por partes, x = u, . Logo, como

Então,

Agora, seja

Sendo

Assim,

.