Hoje vamos falar de Transformações Lineares, com um foco específico nas transformações onde o espaço domínio (aqui sempre tratado como E) tem dimensão infinita. Um espaço vetorial nada mais é que um conjunto fechado por somas e por multiplicação por escalares (reais ou complexos, dependendo do caso), e a dimensão do espaço vetorial é definida como a cardinalidade da base deste espaço.
(Aviso: ao leitor sem familiaridade com um pouco de álgebra linear ou análise em nível elementar, recomendamos que espere um pouco e leia o artigo depois de ter mais segurança nesses conceitos)
Uma transformação linear T entre espaços vetoriais E e F é definida como um mapa entre esses espaços satisfazendo
Quando o espaço E=F, dizemos que T é um operador linear, e quando F é o conjunto dos reais, dizemos que T é um funcional linear.
Comecemos com alguns teoremas básicos da teoria mais elementar das transformações lineares:
Proposição 1: Sejam E,F espaços vetoriais normados (isto é, cada um admite uma norma). Então são equivalentes:
(i)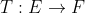 é contínua
é contínua
(ii) 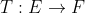 é contínua em um ponto.
é contínua em um ponto.
(iii) 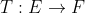 é limitada (isto é, leva conjuntos limitados em conjuntos limitados)
é limitada (isto é, leva conjuntos limitados em conjuntos limitados)
Demonstração: 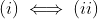 : Se (i) vale, obviamente vale (ii). Se T é contínua em um ponto y de E, então, dada
: Se (i) vale, obviamente vale (ii). Se T é contínua em um ponto y de E, então, dada 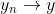 , temos que
, temos que 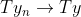 . Suponhamos que temos um outro x em E e uma sequência
. Suponhamos que temos um outro x em E e uma sequência  . Como a sequência
. Como a sequência  , então
, então  . Mas isto equivale a
. Mas isto equivale a 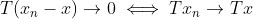 , e assim T é contínua em todo o E.
, e assim T é contínua em todo o E.
Corolário 1: Se E tem dimensão finita, então toda transformação linear de E em F é contínua.
Demonstração: Basta mostrar que T como acima é limitada, pela Prop. 1. Mas isto é fácil: Seja 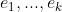 uma base de E com cada um dos elementos tendo norma 1. Como um espaço de dimensão finita k é isomorfo ao
uma base de E com cada um dos elementos tendo norma 1. Como um espaço de dimensão finita k é isomorfo ao 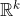 , podemos considerar a norma do máximo em
, podemos considerar a norma do máximo em 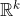 como a norma de E. Assim, se |x| é menor ou igual a 1 em E,
como a norma de E. Assim, se |x| é menor ou igual a 1 em E,  . Logo, T é limitada, e, então, contínua.
. Logo, T é limitada, e, então, contínua. 
Vamos construir um exemplo onde E tem dimensão infinita, para obter um funcional T não contínuo em E.
Seja E o espaço vetorial das sequências onde todos menos um número finito de termos é zero. Se
o conjunto desses elementos forma uma base de E. Além disso, se definirmos um funcional nos elementos de uma base, definimo-no em todo o espaço. Logo, defina T como 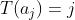 . Considerando no espaço E a norma dada pela soma dos módulos dos termos da sequência, então todos os termos acima definidos têm norma 1, e, portanto, T não é limitada neste conjunto, que obviamente é limitado. Logo, T não pode ser contínua.
. Considerando no espaço E a norma dada pela soma dos módulos dos termos da sequência, então todos os termos acima definidos têm norma 1, e, portanto, T não é limitada neste conjunto, que obviamente é limitado. Logo, T não pode ser contínua.
Para finalizar esta primeira parte, vejamos um resultado importante:
Definição 1: Um espaço vetorial normado é dito um espaço de Banach se, dada uma sequência 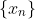 de Cauchy, então esta sequência é convergente, ou seja, existe
de Cauchy, então esta sequência é convergente, ou seja, existe 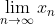 .
.
Definição 2: Dados E,F espaços vetoriais normados, defina L(E;F) como o espaço dos mapas lineares limitados (contínuos) de E em F.
Proposição 2: Se F é um espaço de Banach, L(E;F) também o é.
Demonstração: Exercício. (Dica: Use que F é Banach para achar a T desejada como limite pontual, e aí use a limitação para provar que T é contínua e que a sequência de fato converge a T)
Boa postagem, uma boa introdução à Análise Funcional.
ResponderExcluirOutro bom exercício é mostrar que todo espaço de dimensão finita é Banach.
E um dos fatos mais impressionantes em dimensão finita: Mostrar que a bola unitária fechada não é compacta!
Espero ver logo a parte II, III, ... (até onde?)
Até mais !
Este comentário foi removido pelo autor.
ExcluirPor que você removeu o comentário?
ExcluirOpa, Diego, tudo bem? O comentário foi enviado com um erro, sem uma parte... Por isso removi.
ExcluirEnfim, esqueci de postar de novo (pura preguiça). Mas era somente pra agradecer pelo comentário, dizer que sim, teremos (bem) mais posts sobre Análise Funcional (disciplina que estou cursando agora no mestrado do IMPA, no verão) e que este exercício que você propôs é um clássico, não pode faltar no repertório de qualquer curso respeitável de análise funcional.
Um abraço!
João.
olá, boa tarde. eu tive uma pequena dúvida em relação a demonstração (i) <= (ii) (a volta).
ResponderExcluirVocê utiliza a seguinte sequência: xn - x + y -> y. Então a minha dúvida é se essa é a sequência correta. Pois imagiva que essa seria a sequência correta xn - x + yn -> y. Me tire essa dúvida.
Seu conteúdo é ótimo.
Um abraço.
Anteciosamente,
Luciano Junior